题目内容
已知双曲线C1和椭圆C2: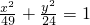 有公共的焦点,它们的离心率分别是e1和e2,且
有公共的焦点,它们的离心率分别是e1和e2,且 ,求双曲线C1的方程.
,求双曲线C1的方程.
解:椭圆方程 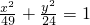 得
得
∴c1=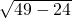 =5
=5
∴焦点坐标为(5,0)(-5,0),离心率e1=
∴设双曲线方程为
则半焦距c2=5
由于
∴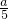 +
+ =2,a=3
=2,a=3
b= =4
=4
∴双曲线方程为
分析:先根据椭圆的方程求得焦点坐标和离心率,进而可知双曲线的半焦距,设出双曲线的标准方程,根据离心率 求得a,再利用c求得b.答案可得.
求得a,再利用c求得b.答案可得.
点评:本题主要考查了双曲线的标准方程..在求曲线方程的问题中,巧设方程,减少待定系数,是非常重要的方法技巧.特别是具有公共焦点的两种曲线,它们的公共点同时具有这两种曲线的性质,解题时要充分注意.
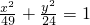 得
得∴c1=
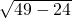 =5
=5∴焦点坐标为(5,0)(-5,0),离心率e1=

∴设双曲线方程为

则半焦距c2=5
由于

∴
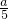 +
+ =2,a=3
=2,a=3b=
 =4
=4∴双曲线方程为

分析:先根据椭圆的方程求得焦点坐标和离心率,进而可知双曲线的半焦距,设出双曲线的标准方程,根据离心率
 求得a,再利用c求得b.答案可得.
求得a,再利用c求得b.答案可得.点评:本题主要考查了双曲线的标准方程..在求曲线方程的问题中,巧设方程,减少待定系数,是非常重要的方法技巧.特别是具有公共焦点的两种曲线,它们的公共点同时具有这两种曲线的性质,解题时要充分注意.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目

 有公共的焦点,它们的离心率分别是e1和e2,且
有公共的焦点,它们的离心率分别是e1和e2,且 ,求双曲线C1的方程.
,求双曲线C1的方程.