题目内容
12.在△ABC中,内角A、B、C的对边分别是a、b、c,若c2=(a-b)2+6,△ABC的面积为$\frac{3\sqrt{3}}{2}$,则C=$\frac{π}{3}$.分析 先化简c2=(a-b)2+6得c2=a2+b2-2ab+6,由余弦定理得c2=a2+b2-2abcosC,两式结合得abcosC=ab-3,由题意和三角形的面积公式列出方程,由平方关系进行化简求出ab、cosC的值,由C的范围和特殊角的余弦值求出C.
解答 解:由题意得,c2=(a-b)2+6,
则c2=a2+b2-2ab+6,
由余弦定理得,c2=a2+b2-2abcosC,
代入上式可得,abcosC=ab-3,①
因为△ABC的面积为$\frac{3\sqrt{3}}{2}$,
所以$\frac{1}{2}absinC=\frac{3\sqrt{3}}{2}$,则absinC=3$\sqrt{3}$,②
①2+②2得,(ab)2=(ab-3)2+27,
化简得,ab=6,代入①得cosC=$\frac{1}{2}$,
由0<C<π得C=$\frac{π}{3}$,
故答案为:$\frac{π}{3}$.
点评 本题考查余弦定理,平方关系,三角形的面积公式,以及化简、变形能力,属于中档题.

练习册系列答案
相关题目
2. 如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在A点测得公路北侧山顶D的仰角为30°,汽车行驶300m后到达B点测得山顶D恰好在正北方,且仰角为45°,则山的高度CD为( )
如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在A点测得公路北侧山顶D的仰角为30°,汽车行驶300m后到达B点测得山顶D恰好在正北方,且仰角为45°,则山的高度CD为( )
 如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在A点测得公路北侧山顶D的仰角为30°,汽车行驶300m后到达B点测得山顶D恰好在正北方,且仰角为45°,则山的高度CD为( )
如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在A点测得公路北侧山顶D的仰角为30°,汽车行驶300m后到达B点测得山顶D恰好在正北方,且仰角为45°,则山的高度CD为( )| A. | 150$\sqrt{2}$ | B. | 150$\sqrt{3}$ | C. | 300$\sqrt{2}$ | D. | 300$\sqrt{3}$ |
7.如图所示,程序框图输出的结果为( )
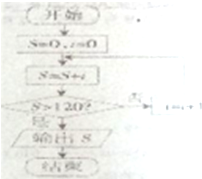

| A. | 15 | B. | 16 | C. | 136 | D. | 153 |
17.游客从某旅游景区的景点A处至景点C处有两条线路,线路1是从A沿直线步行到C,线路2是先从A沿直线步行到景点B处,然后从B沿直线步行道C,现有甲乙两位游客从A处同时出发匀速步行,甲的速度是乙的速度的$\frac{11}{9}$倍,甲走线路2,乙走线路1,最后他们同时到达C处,经测量,AB=1040m,BC=500m,则sin∠BAC等于( )
| A. | $\frac{5}{13}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{7}{24}$ |
2.已知等差数列{an}的前n项和为Sn,且a2=18-a7,S8=( )
| A. | 18 | B. | 36 | C. | 54 | D. | 72 |