题目内容
若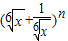
展开式中第二、三、四项的二项式系数成等差数列．（1）求n的值；
（2）此展开式中是否有常数项，为什么？
【答案】分析：（1）由题意可得，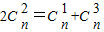
，解方程可求n
（2）先写出二项展开式的通项，然后令x的次方为0，求出r即可判断
解答：解：（1）由题意可得，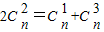
∴
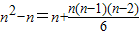
化简可得，n2-9n+14=0
∵n≥3
∴n=7
（2）无常数项，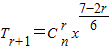
其中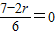
时r=3.5∉Z，故不存在
点评：本题主要考查了二项展开式的系数性质及展开式的通项的应用，解题的关键是熟练掌握基本知识．
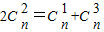，解方程可求n（2）先写出二项展开式的通项，然后令x的次方为0，求出r即可判断
解答：解：（1）由题意可得，
∴
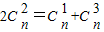
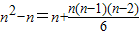
化简可得，n2-9n+14=0
∵n≥3
∴n=7
（2）无常数项，
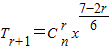
其中
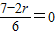时r=3.5∉Z，故不存在点评：本题主要考查了二项展开式的系数性质及展开式的通项的应用，解题的关键是熟练掌握基本知识．
练习册系列答案
相关题目
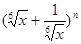展开式中第二、三、四项的二项式系数成等差数列．
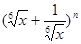展开式中第二、三、四项的二项式系数成等差数列．
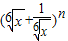展开式中第二、三、四项的二项式系数成等差数列．