题目内容
(12分)若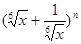 展开式中第二、三、四项的二项式系数成等差数列.
展开式中第二、三、四项的二项式系数成等差数列.
求n的值;
(2)此展开式中是否有常数项,为什么?
【答案】
(1)n =7;(2)无常数项.
【解析】
试题分析:(1)因为展开式中第二、三、四项的二项式系数成等差数列.所以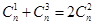 ,解得n =7 (6分)
,解得n =7 (6分)
(2)利用二项展开式写出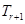 ,令其
,令其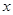 系数为0,无正整数解,所以无常数项(6分)
系数为0,无正整数解,所以无常数项(6分)
考点:本题主要考查二项式定理、二项式展开式即等差数列的性质。
点评:基本题型,考查二项式定理的同时,综合考查考生的计算能力。

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
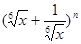 展开式中第二、三、四项的二项式系数成等差数列.
展开式中第二、三、四项的二项式系数成等差数列.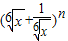 展开式中第二、三、四项的二项式系数成等差数列.
展开式中第二、三、四项的二项式系数成等差数列.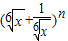 展开式中第二、三、四项的二项式系数成等差数列.
展开式中第二、三、四项的二项式系数成等差数列.