题目内容
设a>0为常数,动点M(x,y)(y≠0)分别与两定点F1(-a,0),F2(a,0)的连线的斜率之积为定值λ,若点M的轨迹是离心率为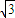 双曲线,则λ的值为( )
双曲线,则λ的值为( )A.2
B.-2
C.3
D.
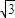
【答案】分析:根据题意可分别表示出动点P与两定点的连线的斜率,根据其之积为常数,求得x和y的关系式,对k的范围进行分类讨论,看k>0根据圆锥曲线的标准方程可推断出离心率,从而求得λ的值.
解答:解:依题意可知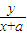 •
•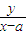 =λ,整理得y2-λx2=-λa2,
=λ,整理得y2-λx2=-λa2,
当λ>0时,方程的轨迹为双曲线,
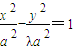
∴b2=λa2,c=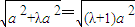
∴e=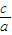 =
=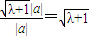 =
=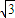
∴λ=2
故选A
点评:本题主要考查了圆锥曲线的综合.考查了学生对圆锥曲线标准方程的考查和应用.
解答:解:依题意可知
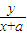 •
•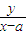 =λ,整理得y2-λx2=-λa2,
=λ,整理得y2-λx2=-λa2,当λ>0时,方程的轨迹为双曲线,
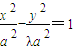
∴b2=λa2,c=
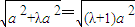
∴e=
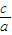 =
=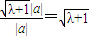 =
=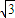
∴λ=2
故选A
点评:本题主要考查了圆锥曲线的综合.考查了学生对圆锥曲线标准方程的考查和应用.

练习册系列答案
相关题目
 (2012•辽宁)如图,已知椭圆C0:
(2012•辽宁)如图,已知椭圆C0: 双曲线,则λ的值为
双曲线,则λ的值为