Question

【题目】分别求适合下列条件的椭圆的标准方程.
（1）焦点在坐标轴上，且经过点A ( ,-2),B(-2 ,1)；
（2）与椭圆 有相同焦点且经过点M( ,1).

Answer 1

【答案】
（1）解：设所求椭圆的方程为mx2+ny2=1（m＞0，n＞0，且m≠n），根据题意可得：
，
解得 ，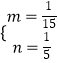
∴所求椭圆的标准方程为 + =1.
（2）解：由椭圆 ,可以知道焦点在x轴上,
, , ,则
椭圆C的两焦点分别为: 和 ,
设椭圆C的方程为: ,
把 代入方程,得 ,
即 ,
或 (舍),
椭圆C的方程为: .
【解析】（1）因为椭圆的焦点位置不确定，故不能直接设a，b，可以先设为m，n，将两点坐标代入解出m和n的值即可。
（2）根据已知椭圆方程求出c的值，然后设出要求的椭圆方程，将点M的坐标代入，解出a的值，即可得到方程。