题目内容
14．等比数列{an}中，前n项和Sn=3n+r，则r=-1，公比q=3，通项公式an=2•3n-1．分析 由等比数列的前n项和求出前3项，结合等比数列的性质求得r，进一步求得q，然后代入等比数列的通项公式得答案．
解答 解：由Sn=3n+r，得
a1=S1=3+r，a2=S2-S1=9+r-3-r=6，a3=S3-S2=27+r-9-r=18，
∵{an}为等比数列，
∴62=（3+r）•18，解得r=-1．
a1=3-1=2，
q=$\frac{{a}_{2}}{{a}_{1}}=\frac{6}{2}=3$，
∴${a}_{n}={a}_{1}•{q}^{n-1}=2•{3}^{n-1}$．
故答案为：-1；3；2•3n-1．
点评 本题考查了等比数列的性质，考查了等比数列的前n项和，是基础题．
练习册系列答案
相关题目
2．已知i为虚数单位，集合A={1，2，zi}，B={1，3}，A∪B={1，2，3，4}，则复数z=（ ）
| A． | -4i | B． | 4i | C． | -2i | D． | 2i |
9．
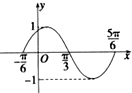函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在[-$\frac{π}{6}$，$\frac{5π}{6}$]的图象如图所示，为了得到这个函数的图象，只要将f（x）=sinωx的图象（ ）
函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在[-$\frac{π}{6}$，$\frac{5π}{6}$]的图象如图所示，为了得到这个函数的图象，只要将f（x）=sinωx的图象（ ）| A． | 向右平移$\frac{π}{3}$个单位长度 | B． | 向右平移$\frac{π}{6}$个单位长度 | ||
| C． | 向左平移$\frac{π}{3}$个单位长度 | D． | 向左平移$\frac{π}{6}$个单位长度 |
3．已知命题p：“存在x0∈[1，+∞），使得（log23）${\;}^{{x}_{0}}$≥1”，则下列说法正确的是（ ）
| A． | p是假命题；￢p“任意x∈[1，+∞），都有（log23）x＜1” | |
| B． | p是真命题；￢p“不存在x0∈[1，+∞），使得（log23）${\;}^{{x}_{0}}$＜1” | |
| C． | p是真命题；￢p“任意x∈[1，+∞），都有（log23）x＜1” | |
| D． | p是假命题；￢p“任意x∈（-∞，1），都有（log23）x＜1” |