题目内容
对于集合M、N,定义M-N={x|x∈M且x∉N},M⊕N=(M-N)∪(N-M),设A={y|y=3x,x∈R},B={y|y=-(x-1)2+2,x∈R},则A⊕B等于( )
| A．[0,2) |
| B．(0,2] |
| C．(-∞,0]∪(2,+∞) |
| D．(-∞,0)∪[2,+∞) |
C
由题可知,集合A={y|y>0},B={y|y≤2},
所以A-B={y|y>2},B-A={y|y≤0},
所以A⊕B=(-∞,0]∪(2,+∞).故选C.
所以A-B={y|y>2},B-A={y|y≤0},
所以A⊕B=(-∞,0]∪(2,+∞).故选C.
练习册系列答案
相关题目
，集合
，
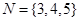，则
( )
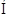B，求实数a的取值范围．
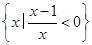,B={x|x≥1},则集合{x|x≤0}等于( )
.
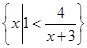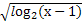},B={y|y=
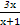},则A∩B=( )