题目内容
已知函数y=tan（2x+ϕ）的图象过点
，则φ的值可以为（ ）A．
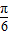
B．
C．
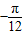
D．
【答案】分析：直接把点的坐标代入函数的表达式，求出φ的值即可．
解答：解：因为函数y=tan（2x+ϕ）的图象过点
，
所以0=tan（2×
+φ），所以φ=k
，k∈Z，
当k=1时，φ=
．
故选A．
点评：本题考查三角函数解析式的应用，函数的参变量的求法，考查计算能力．
解答：解：因为函数y=tan（2x+ϕ）的图象过点
，所以0=tan（2×
+φ），所以φ=k，k∈Z，当k=1时，φ=
．故选A．
点评：本题考查三角函数解析式的应用，函数的参变量的求法，考查计算能力．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
已知函数y=tanωx在(-
，
)上是减函数，则（ ）
| π |
| 2 |
| π |
| 2 |
| A、0＜ω≤1 | B、-1≤ω＜0 |
| C、ω≥1 | D、ω≤-1 |
已知函数y=tan（2x+φ）的图象过点（
，0），则φ可以是（ ）
| π |
| 12 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
已知函数y=tan