Question

（2011•广州模拟）已知实数x，y满足

x≥0 y≤1 2x-2y+1≤0.

，若目标函数z=ax+y（a≠0）取得最小值时最优解有无数个，则实数a的值为（　　）

• A．-1
• B．-

  1

  2

• C．

  1

  2

• D．1

Answer 1

分析：将目标函数z=ax+y化成斜截式方程后得：y=-ax+z，目标函数值Z看成是直线族y=-ax+z的截距，当直线族y=-ax+z的斜率与直线AB的斜率相等时，目标函数z=ax+y取得最小值的最优解有无数多个，由此不难得到a的值．

解答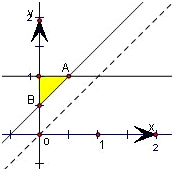：解：∵目标函数z=ax+y，
∴y=-ax+z．
故目标函数值Z是直线族y=-ax+z的截距
当直线族y=-ax+z的斜率与直线AB的斜率相等时，
目标函数z=ax+y取得最小值的最优解有无数多个，
直线AB：2x-2y+1=0的斜率为1，
此时，-a=1
即a=-1
故选A．

点评：本题考查线性规划最优解的判定，属于该知识的逆用题型，利用最优解的特征，判断出最优解的位置求参数，属于基础题．