题目内容
给出下列五个命题:①若f(x)=sin(2x+φ)是偶函数,则
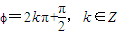 ;
;②函数
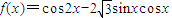 在区间
在区间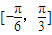 上是单调递增;
上是单调递增;③已知a,b∈R,则“a>b>0”是“
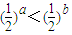 ”的充分不必要条件;
”的充分不必要条件;④若xlog34=1,则
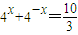 ;
;⑤在△ABC中,若tanA+tanB+tanC>0,则△ABC必为锐角三角形.
其中正确命题的序号是 (写出所有正确命题的序号).
【答案】分析:①由偶函数的性质可得对称轴为y轴且该点取得函数的最值,则f(0)=±1,代入可求φ
②利用辅助角公式化简可得,函数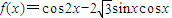 =cos(2x+
=cos(2x+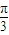 )利用余弦函数的单调性判断
)利用余弦函数的单调性判断
③结合指数函数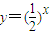 的单调性及定义域判断
的单调性及定义域判断
④由xlog34=1⇒x=log43,代入求解即可
⑤由三角形的内角和定理可知,三角形的内角最多有一个钝角,故可设A,B为锐角,tanA>0,tanB>0
利用内角和公式可把tanA+tanB+tanC>0⇒tanA+tanB-tan(A+B)>0,利用两角和的正切公式展开整理可得tanAtanB>1,则可得tanA>cotB=tan(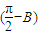 ,则有A
,则有A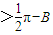 ,所以有A+B
,所以有A+B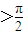 ,从而可得C
,从而可得C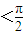
解答:解:①若f(x)=sin(2x+φ)是偶函数,则由偶函数的性质可得对称轴为y轴且该点取得函数的最值,则f(0)=±1,代入可得,φ=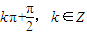 故①错误
故①错误
②函数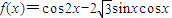 =cos2x
=cos2x =
=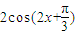 ,在区间
,在区间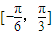 上是单调递减,故②错误
上是单调递减,故②错误
③a>b>0⇒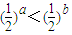 ,但由
,但由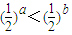 只可得a>b,即a>b>0是
只可得a>b,即a>b>0是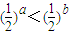 的充分不必要条件,故③正确
的充分不必要条件,故③正确
④由xlog34=1⇒x=log43,则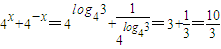 ,故④正确
,故④正确
⑤由三角形的内角和定理可知,三角形的内角最多有一个钝角,故可设A,B为锐角,tanA>0,tanB>0
利用内角和公式可把tanA+tanB+tanC>0⇒tanA+tanB-tan(A+B)>0,利用两角和的正切公式展开整理可得tanAtanB>1,则可得tanA>cotB=tan(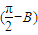 ,则有A
,则有A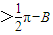 ,所以有A+B
,所以有A+B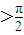 ,从而可得C
,从而可得C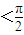 故⑤正确
故⑤正确
故答案为:③④⑤
点评:本题综合考查了正弦函数的奇偶性,三角函数的辅助角公式的运用,指数函数的定义域、单调性及特殊点的应用,对数的换底公式及指数的基本运算,
②利用辅助角公式化简可得,函数
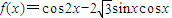 =cos(2x+
=cos(2x+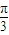 )利用余弦函数的单调性判断
)利用余弦函数的单调性判断③结合指数函数
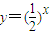 的单调性及定义域判断
的单调性及定义域判断④由xlog34=1⇒x=log43,代入求解即可
⑤由三角形的内角和定理可知,三角形的内角最多有一个钝角,故可设A,B为锐角,tanA>0,tanB>0
利用内角和公式可把tanA+tanB+tanC>0⇒tanA+tanB-tan(A+B)>0,利用两角和的正切公式展开整理可得tanAtanB>1,则可得tanA>cotB=tan(
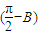 ,则有A
,则有A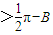 ,所以有A+B
,所以有A+B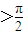 ,从而可得C
,从而可得C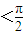
解答:解:①若f(x)=sin(2x+φ)是偶函数,则由偶函数的性质可得对称轴为y轴且该点取得函数的最值,则f(0)=±1,代入可得,φ=
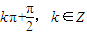 故①错误
故①错误②函数
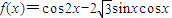 =cos2x
=cos2x =
=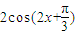 ,在区间
,在区间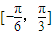 上是单调递减,故②错误
上是单调递减,故②错误③a>b>0⇒
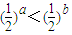 ,但由
,但由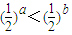 只可得a>b,即a>b>0是
只可得a>b,即a>b>0是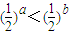 的充分不必要条件,故③正确
的充分不必要条件,故③正确④由xlog34=1⇒x=log43,则
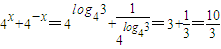 ,故④正确
,故④正确⑤由三角形的内角和定理可知,三角形的内角最多有一个钝角,故可设A,B为锐角,tanA>0,tanB>0
利用内角和公式可把tanA+tanB+tanC>0⇒tanA+tanB-tan(A+B)>0,利用两角和的正切公式展开整理可得tanAtanB>1,则可得tanA>cotB=tan(
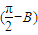 ,则有A
,则有A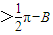 ,所以有A+B
,所以有A+B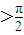 ,从而可得C
,从而可得C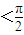 故⑤正确
故⑤正确故答案为:③④⑤
点评:本题综合考查了正弦函数的奇偶性,三角函数的辅助角公式的运用,指数函数的定义域、单调性及特殊点的应用,对数的换底公式及指数的基本运算,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目