题目内容
【题目】下列四个命题:
![]() 函数
函数![]() 的最大值为1;
的最大值为1;
![]() “
“![]() ,
,![]() ”的否定是“
”的否定是“![]() ”;
”;
![]() 若
若![]() 为锐角三角形,则有
为锐角三角形,则有![]() ;
;
![]() “
“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 内单调递增”的充分必要条件.
内单调递增”的充分必要条件.
其中错误的个数是( )
A.1B.2C.3D.4
【答案】A
【解析】
由正弦的二倍角公式和正弦函数的值域判断![]() ;写出全称命题的否定判断
;写出全称命题的否定判断![]() ;由锐角三角形的定义和正弦函数的单调性,结合诱导公式可判断
;由锐角三角形的定义和正弦函数的单调性,结合诱导公式可判断![]() ;由二次函数的图象和性质,结合充分必要条件的定义可判断
;由二次函数的图象和性质,结合充分必要条件的定义可判断![]() .
.
解:![]() 由
由![]() ,得
,得![]() 的最大值为
的最大值为![]() ,故
,故![]() 错误;
错误;
![]() “
“![]() ,
,![]() ”的否定是“
”的否定是“![]() ”,故
”,故![]() 正确;
正确;
![]() 为锐角三角形,
为锐角三角形,![]() ,则
,则![]() ,
,
![]() 在
在![]() 上是增函数,
上是增函数,![]() ,同理可得
,同理可得![]() ,
,![]() ,
,![]() ,故
,故![]() 正确;
正确;
![]() ,函数
,函数![]() 的零点是
的零点是![]() ,0,结合二次函数的对称轴,
,0,结合二次函数的对称轴,
可得函数![]() 在区间
在区间![]() 内单调递增;
内单调递增;
若函数![]() 在区间
在区间![]() 内单调递增,结合二次函数的对称轴,可得
内单调递增,结合二次函数的对称轴,可得![]() ,
,
![]() ,
,
![]() “
“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 内单调递增”的充分必要条件,故
内单调递增”的充分必要条件,故![]() 正确.
正确.
![]() 其中错误的个数是1.
其中错误的个数是1.
故选:A.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】某市房管局为了了解该市市民![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间买二手房情况,首先随机抽样其中
月期间买二手房情况,首先随机抽样其中![]() 名购房者,并对其购房面积
名购房者,并对其购房面积![]() (单位:平方米,
(单位:平方米,![]() )进行了一次调查统计,制成了如图
)进行了一次调查统计,制成了如图![]() 所示的频率分布直方图,接着调查了该市
所示的频率分布直方图,接着调查了该市![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间当月在售二手房均价
月期间当月在售二手房均价![]() (单位:万元/平方米),制成了如图
(单位:万元/平方米),制成了如图![]() 所示的散点图(图中月份代码
所示的散点图(图中月份代码![]() 分别对应
分别对应![]() 年
年![]() 月至
月至![]() 年
年![]() 月).
月).

(1)试估计该市市民的购房面积的中位数![]() ;
;
(2)从该市![]() 年
年![]() 月至
月至![]() 年
年![]() 月期间所有购买二手房中的市民中任取
月期间所有购买二手房中的市民中任取![]() 人,用频率估计概率,记这
人,用频率估计概率,记这![]() 人购房面积不低于
人购房面积不低于![]() 平方米的人数为
平方米的人数为![]() ,求
,求![]() 的数学期望;
的数学期望;
(3)根据散点图选择![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程,分别为
两个模型进行拟合,经过数据处理得到两个回归方程,分别为![]() 和
和![]() ,并得到一些统计量的值如下表所示:
,并得到一些统计量的值如下表所示:
|
| |
|
|
|
|
| |
请利用相关指数![]() 判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出
判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测出![]() 年
年![]() 月份的二手房购房均价(精确到
月份的二手房购房均价(精确到![]() )
)
(参考数据)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(参考公式)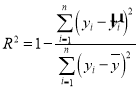 .
.