题目内容
18.设函数f(x)=$\sqrt{3}$sinωx+cosωx-1(ω>0),且满足相邻两个最大值间的距离为π;(1)求ω
(2)若y=f(x)的图象向右平移a(a>0)个单位,图象再向上移动一个单位得到y=g(x)的图象,且y=g(x)为奇函数,求a的最小值.
分析 (1)由条件利用两角和差的正弦公式化简函数f(x)的解析式,再利用正弦函数的图象性质求得ω的值.
(2)由条件利用y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:(1)由函数f(x)=$\sqrt{3}$sinωx+cosωx-1=2sin(ωx+$\frac{π}{6}$)-1(ω>0),
且满足相邻两个最大值间的距离为π,可得$\frac{2π}{ω}$=π,
求得ω=2,f(x)=2sin(2x+$\frac{π}{6}$)-1.
(2)把y=f(x)的图象向右平移a(a>0)个单位,
可得y=2sin[2(x-a)+$\frac{π}{6}$]-1=2sin(2x-2a+$\frac{π}{6}$)-1的图象;
图象再向上移动一个单位得到y=g(x)=2sin(2x-2a+$\frac{π}{6}$) 的图象,
再根据y=g(x)为奇函数,则-2a+$\frac{π}{6}$=kπ,k∈Z,故a的最小值为$\frac{π}{12}$.
点评 本题主要考查两角和差的正弦公式,正弦函数的图象性质,y=Asin(ωx+φ)的图象变换规律,属于基础题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x-y≤1}\\{2x+y≤5}\\{x≥1}\end{array}\right.$,则z=-3x+y的最小值为( )
| A. | -4 | B. | -5 | C. | -6 | D. | -7 |
10.已知$\vec a=({-3,2}),\vec b=({-1,0})$,向量λ$\vec a+\vec b$与$\overrightarrow{a}$-$\overrightarrow{b}$垂直,则实数λ的值为( )
| A. | $\frac{1}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{1}{7}$ | D. | $-\frac{1}{7}$ |
7.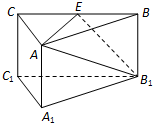 如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
 如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | AC⊥平面ABB1A1 | ||
| C. | A1C1∥平面AB1E | D. | AE,B1C1为异面直线,且AE⊥B1C1 |