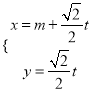Question

【题目】已知g（x）=﹣x2﹣3，f（x）是二次函数，f（x）+g（x）是奇函数，且当x∈[﹣1，2]时，f（x）的最小值为1，求f（x）的表达式．

Answer 1

【答案】解：设f（x）=ax2+bx+c（a≠0）
则g（x）+f（x）=（a﹣1）x2+bx+c﹣3为奇函数，
∴a=1，c=3（4分）
∴ ∵当x∈[﹣1，2]时f（x）的最小值为1
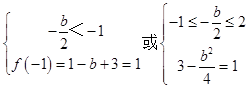∴ 或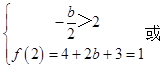
解得b=3或
∴
故f（x）的表达式为：
【解析】用待定系数法求函数f（x）的解析式，设f（x）=ax2+bx+c（a≠0），利用奇函数的定义列等式，利用二次函数的最值列不等式，从而求出系数即可．
【考点精析】根据题目的已知条件，利用函数的奇偶性的相关知识可以得到问题的答案，需要掌握偶函数的图象关于y轴对称；奇函数的图象关于原点对称．