题目内容

若函数f（x）=|4x-x2|-a的零点个数为2，则a的范围是
{a|a=0或a＞4}
{a|a=0或a＞4}
．
分析：令g（x）=|4x-x2|=
x2-4x，x≥4或x≤0
4x-x2，0＜x＜4
，画出函数g（x）的图象；当x=2时，g（2）=4．当x=0或4时，g（0）=g（4）=0．即可得出a的取值范围．
解答：解：令g（x）=|4x-x2|=
x2-4x，x≥4或x≤0
4x-x2，0＜x＜4
，
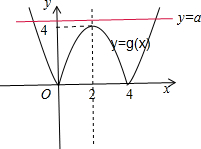
画出函数g（x）的图象，
当x=2时，g（2）=4．当x=0或4时，g（0）=g（4）=0．
∴当a=0或a＞4时，函数f（x）=|4x-x2|-a的零点个数为2．
故答案为：{a|a=0或a＞4}．
点评：本题考查了二次函数的图象与性质、含绝对值符号的函数的图象、数形结合等基础知识与基本技能方法，属于中档题．
练习册系列答案
相关题目
若函数f（x）=4×9-|x-2|-2（P-2）×3-|x-2|-2P2-P+1在区间[2，+∞）内至少存在一个实数c使f（c）＞0，则实数P的取值范围是
 
．
若函数f（x）=|4-x2|的定义域为[a，b]，值域为[0，2]，定义区间[a，b]的长度为b-a，则区间[a，b]长度的最小值为
 
．
若函数f（x）=4+ax（a＞0且a≠1）在[1，2]上的最大值比最小值大
a2
，求a的值．
若函数f（x）=4×9-|x-2|-2（P-2）×3-|x-2|-2P2-P+1在区间[2，+∞）内至少存在一个实数c使f（c）＞0，则实数P的取值范围是______．
已知a>0且a≠1，f（loga x）=（x-）.

（1）试证明函数y=f（x）的单调性.

（2）是否存在实数m满足：当y=f（x）的定义域为（-1，1）时，有f（1-m）+f（1-m2）＜0?若存在，求出其取值范围；若不存在，请说明理由.

（3）若函数f（x）-4恰好在（-∞，2）上取负值，求a的值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网