题目内容
【题目】设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x
B.y2=2x或y2=8x
C.y2=4x或y2=16x
D.y2=2x或y2=16x
【答案】C
【解析】解:∵抛物线C方程为y2=2px(p>0),
∴焦点F坐标为( ![]() ,0),可得|OF|=
,0),可得|OF|= ![]() ,
,
∵以MF为直径的圆过点(0,2),
∴设A(0,2),可得AF⊥AM,
Rt△AOF中,|AF|= ![]() =
= ![]() ,
,
∴sin∠OAF= ![]() =
= ![]() ,
,
∵根据抛物线的定义,得直线AO切以MF为直径的圆于A点,
∴∠OAF=∠AMF,可得Rt△AMF中,sin∠AMF= ![]() =
= ![]() ,
,
∵|MF|=5,|AF|= ![]()
∴ ![]() =
= ![]() ,整理得4+
,整理得4+ ![]() =
= ![]() ,解之可得p=2或p=8
,解之可得p=2或p=8
因此,抛物线C的方程为y2=4x或y2=16x.
故选:C.
方法二:
∵抛物线C方程为y2=2px(p>0),∴焦点F( ![]() ,0),
,0),
设M(x,y),由抛物线性质|MF|=x+ ![]() =5,可得x=5﹣
=5,可得x=5﹣ ![]() ,
,
因为圆心是MF的中点,所以根据中点坐标公式可得,圆心横坐标为 ![]() =
= ![]() ,
,
由已知圆半径也为 ![]() ,据此可知该圆与y轴相切于点(0,2),故圆心纵坐标为2,则M点纵坐标为4,
,据此可知该圆与y轴相切于点(0,2),故圆心纵坐标为2,则M点纵坐标为4,
即M(5﹣ ![]() ,4),代入抛物线方程得p2﹣10p+16=0,所以p=2或p=8.
,4),代入抛物线方程得p2﹣10p+16=0,所以p=2或p=8.
所以抛物线C的方程为y2=4x或y2=16x.
故答案C.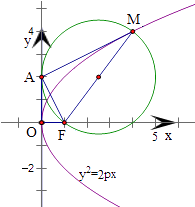

 每课必练系列答案
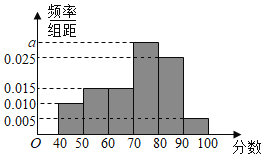
每课必练系列答案【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名高三学生平均每天课外体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟)
平均每天锻炼的时间/分钟 |
|
|
|
|
|
|
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均课外体育锻炼时间在![]() 的学生评价为“课外体育达标”.
的学生评价为“课外体育达标”.
(1)请根据上述表格中的统计数据填写下面的![]() 列联表;
列联表;
课外体育不达标 | 课外体育达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
(2)通过计算判断是否能在犯错误的概率不超过![]() 的前提下认为“课外体育达标”性别有关?
的前提下认为“课外体育达标”性别有关?
参考公式![]() ,其中
,其中![]()
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】通过随机询问110名不同的大学生是否爱好某项运动,得到如下的列联表:
经计算![]() 的观测值
的观测值![]() . 参照附表,得到的正确结论是
. 参照附表,得到的正确结论是
附表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A. 有99%以上的把握认为“爱好该项运动与性别有关”
B. 有99%以上的把握认为“爱好该项运动与性别无关”
C. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”