Question

【题目】对于棱长为的正方体，有如下结论，其中错误的是（ ）

A. 以正方体的顶点为顶点的几何体可以是每个面都为直角三角形的四面体；

B. 过点作平面的垂线，垂足为点，则三点共线；

C. 过正方体中心的截面图形不可能是正六边形；

D. 三棱锥与正方体的体积之比为．

Answer 1

【答案】C

【解析】

在正方体中可找到四面体各个面都是直角三角形，排除；利用线面垂直判定定理可证出平面，从而可知三点共线，排除；在图形中可找到截面图形为正六边形的情况，可知结果为；利用切割的方法求得，从而可求得所求体积之比，排除.

在如下图所示的正方体中：

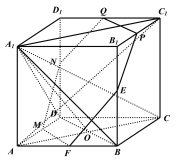
四面体的四个面均为直角三角形，可知正确；

， 平面

又

，即

平面，即过作平面的垂线即为

三点共线，可知正确；

若为所在棱的中点，连接后可知六边形为正六边形且此正六边形过正方体的中心，可知错误；

三棱锥体积：

正方体体积：

三棱锥与正方体的体积之比为：，可知正确.

本题正确选项：