题目内容
【题目】为培养学生对传统文化的兴趣,某校从理科甲班抽取60人,从文科乙班抽取50人参加传统文化知识竞赛.
(1)根据题目条件完成下边![]() 列联表,并据此判断是否有99%的把握认为学生的传统文化知识竞赛成绩优秀与文理分科有关.
列联表,并据此判断是否有99%的把握认为学生的传统文化知识竞赛成绩优秀与文理分科有关.
优秀人数 | 非优秀人数 | 总计 | |
甲班 | |||
乙班 | 20 | ||
总计 | 60 |
(2)现已知![]() ,
,![]() ,
,![]() 三人获得优秀的概率分别为
三人获得优秀的概率分别为![]() ,
,![]() ,
,![]() ,设随机变量
,设随机变量![]() 表示
表示![]() ,
,![]() ,
,![]() 三人中获得优秀的人数,求
三人中获得优秀的人数,求![]() 的分布列及期望
的分布列及期望![]() .
.
附: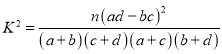 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【答案】(1)表格见解析,有99%的把握认为学生的传统文化知识竞赛成绩优秀与文理分科有关;(2)分布列见解析,![]() .
.
【解析】
(1)先计算出乙班非优秀人数,填空两班总计数,及非优秀人数的总计,然后可计算出甲班优秀人数和非优秀人数,得列联表,根据公式计算出![]() 后可得结论;
后可得结论;
(2)记![]() ,
,![]() ,
,![]() 成绩优秀分别为事件
成绩优秀分别为事件![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]()
随机变量![]() 的取值为0,1,2,3.根据独立事件的概率公式分别计算出概率得分布列,然后可计算出期望.
的取值为0,1,2,3.根据独立事件的概率公式分别计算出概率得分布列,然后可计算出期望.
解:(1)![]() 列联表如下:
列联表如下:
优秀人数 | 非优秀人数 | 总计 | |
甲班 | 40 | 20 | 60 |
乙班 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由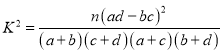 ,
,
得 ,
,
所以有99%的把握认为学生的传统文化知识竞赛成绩优秀与文理分科有关.
(2)记![]() ,
,![]() ,
,![]() 成绩优秀分别为事件
成绩优秀分别为事件![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]()
随机变量![]() 的取值为0,1,2,3.
的取值为0,1,2,3.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
所以随机变量![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() .
.

【题目】科研人员在对人体脂肪含量和年龄之间关系的研究中,获得了一些年龄和脂肪含量的简单随机样本数据,如下表:
| 26 | 27 | 39 | 41 | 49 | 53 | 56 | 58 | 60 | 61 |
| 14.5 | 17.8 | 21.2 | 25.9 | 26.3 | 29.6 | 31.4 | 33.5 | 35.2 | 34.6 |
根据上表的数据得到如下的散点图.
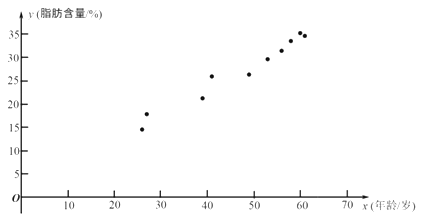
(1)根据上表中的样本数据及其散点图:
(i)求![]() ;
;
(i)计算样本相关系数(精确到0.01),并刻画它们的相关程度.
(2)若![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,求
,求![]() 的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量.
附:参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数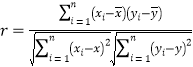
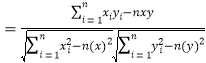
回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为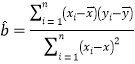 ,
,![]() .
.
【题目】为加快新能源汽车产业发展,推进节能减排,某年国家对消费者购买新能源汽车给予补贴,其中对纯电动乘用车补贴标准如下表:
新能源汽车补贴标准 | |||
车辆类型 | 续驶里程 | ||
|
|
| |
纯电动乘用车 | 3.5万元/辆 | 5万元/辆 | 6万元/辆 |
某校研究学习小组从汽车市场上随机选取了![]() 辆纯电动乘用车,根据其续驶里程
辆纯电动乘用车,根据其续驶里程![]() (单次充电后能行驶的最大里程)作出了如下的频率与频数的统计表:
(单次充电后能行驶的最大里程)作出了如下的频率与频数的统计表:
分组 | 频数 | 频率 |
| 2 | 0.2 |
| 5 |
|
|
|
|
合计 |
| 1 |
(1)若从这![]() 辆纯电动乘用车中任选2辆,求选到的2辆车续驶里程都不低于150km的概率.
辆纯电动乘用车中任选2辆,求选到的2辆车续驶里程都不低于150km的概率.
(2)若以频率作为概率,设![]() 为购买一辆纯电动乘用车获得的补贴,求
为购买一辆纯电动乘用车获得的补贴,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.