题目内容
(本小题满分14分)已知定义在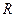 上的函数
上的函数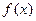 ,满足条件:①
,满足条件:①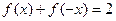 ,②对非零实数
,②对非零实数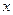 ,都有
,都有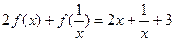 .
.
(1)求函数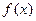 的解析式;
的解析式;
(2)设函数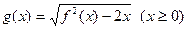 ,直线
,直线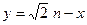 分别与函数
分别与函数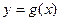 ,
,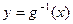 交于
交于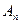 、
、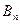 两点,(其中
两点,(其中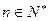 );设
);设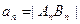 ,
,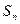 为数列
为数列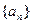 的前
的前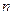 项和,求证:当
项和,求证:当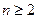 时,
时,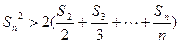 .
.
 上的函数
上的函数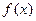 ,满足条件:①
,满足条件:①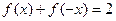 ,②对非零实数
,②对非零实数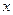 ,都有
,都有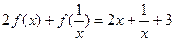 .
.(1)求函数
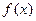 的解析式;
的解析式;(2)设函数
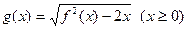 ,直线
,直线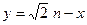 分别与函数
分别与函数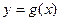 ,
,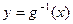 交于
交于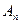 、
、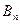 两点,(其中
两点,(其中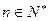 );设
);设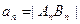 ,
,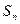 为数列
为数列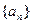 的前
的前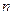 项和,求证:当
项和,求证:当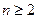 时,
时,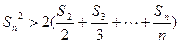 .
.解:(1)当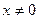 时,
时,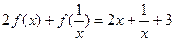
故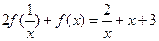 两式联立
两式联立
可得,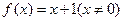
又当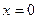 时,有
时,有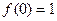 ;
;
∴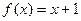 。 ----------------4分
。 ----------------4分
(2)由(1)可得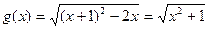 ,
,
联立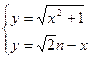 得交点
得交点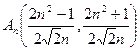 , ----------------6分
, ----------------6分
由此得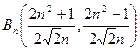 , ----------7分
, ----------7分
所以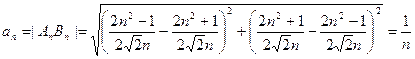 ------9分
------9分
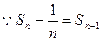
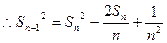 , ------------10分
, ------------10分
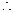 当
当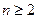 时,
时,
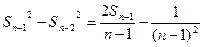
……
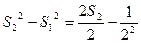
累加得: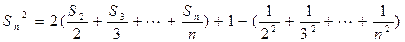 ------12分
------12分
又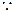
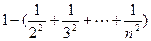
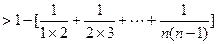
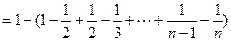
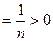
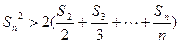 -----------------14分
-----------------14分
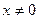 时,
时,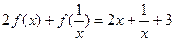
故
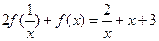 两式联立
两式联立可得,
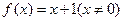
又当
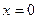 时,有
时,有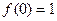 ;
;∴
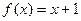 。 ----------------4分
。 ----------------4分(2)由(1)可得
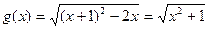 ,
,联立
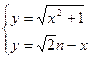 得交点
得交点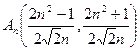 , ----------------6分
, ----------------6分由此得
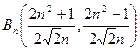 , ----------7分
, ----------7分 所以
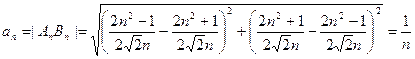 ------9分
------9分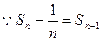
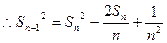 , ------------10分
, ------------10分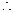 当
当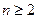 时,
时,
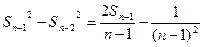
……
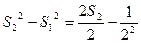
累加得:
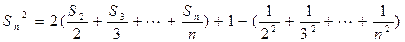 ------12分
------12分又
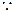
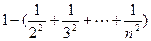
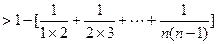
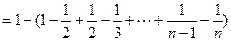
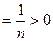
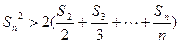 -----------------14分
-----------------14分
略

练习册系列答案
相关题目
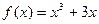 ,
,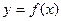 在点
在点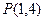 处
处 的切线方程;
的切线方程;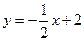 ,则
,则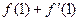 等于( )
等于( )
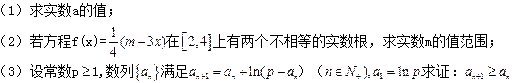
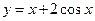 在区间
在区间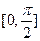 上的最大值是
上的最大值是 

 的定义域为开区间
的定义域为开区间 ,导函数
,导函数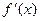 在
在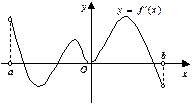

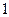 个 B
个 B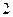 个 C
个 C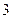 个 D
个 D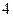 个
个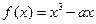 在区间
在区间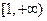 上是单调增函数,则
上是单调增函数,则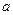 的最大值为 ( )
的最大值为 ( )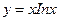 在
在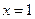 处的切线方程为 .
处的切线方程为 .