题目内容
(2013•山东)椭圆C:
+
=1(a>0,b>0)的左右焦点分别是F1,F2,离心率为
,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,连接PF1,PF2,设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围;
(3)在(2)的条件下,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点,设直线PF1,PF2的斜率分别为k1,k2,若k≠0,试证明
+
为定值,并求出这个定值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,连接PF1,PF2,设∠F1PF2的角平分线PM交C的长轴于点M(m,0),求m的取值范围;
(3)在(2)的条件下,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点,设直线PF1,PF2的斜率分别为k1,k2,若k≠0,试证明
| 1 |
| kk1 |
| 1 |
| kk2 |
分析:(1)把-c代入椭圆方程得
+
=1,解得y=±
,由已知过F1且垂直于x轴的直线被椭圆C截得的线段长为1,可得
=1.再利用e=
=
,及a2=b2+c2即可得出;
(2)设|PF1|=t,|PF2|=n,由角平分线的性质可得
=
=
,利用椭圆的定义可得t+n=2a=4,消去t得到
=
,化为n=
,再根据a-c<n<a+c,即可得到m的取值范围;
(3)设P(x0,y0),不妨设y0>0,由椭圆方程
+y2=1,取y=
,利用导数即可得到切线的斜率,再利用斜率计算公式即可得到k1,k2,代入即可证明结论.
| c2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
| 2b2 |
| a |
| c |
| a |
| ||
| 2 |
(2)设|PF1|=t,|PF2|=n,由角平分线的性质可得
| t |
| n |
| |MF1| |
| |F2M| |
m+
| ||
|
| 4-n |
| n |
| ||
|
2(
| ||
|
(3)设P(x0,y0),不妨设y0>0,由椭圆方程
| x2 |
| 4 |
1-
|
解答:解:(1)把-c代入椭圆方程得
+
=1,解得y=±
,
∵过F1且垂直于x轴的直线被椭圆C截得的线段长为1,∴
=1.
又e=
=
,联立得
解得
,
∴椭圆C的方程为
+y2=1.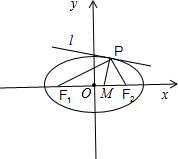
(2)如图所示,设|PF1|=t,|PF2|=n,
由角平分线的性质可得
=
=
,
又t+n=2a=4,消去t得到
=
,化为n=
,
∵a-c<n<a+c,即2-
<n<2+
,也即2-
<
<2+
,解得-
<m<
.
∴m的取值范围;(-
,
).
(3)证明:设P(x0,y0),
不妨设y0>0,由椭圆方程
+y2=1,
取y=
,则y′=
=-
,
∴k=kl=-
=-
.
∵k1=
,k2=
,
∴
+
=
,
∴
+
=-
×
=-8为定值.
| c2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
∵过F1且垂直于x轴的直线被椭圆C截得的线段长为1,∴
| 2b2 |
| a |
又e=
| c |
| a |
| ||
| 2 |
|
|
∴椭圆C的方程为
| x2 |
| 4 |

(2)如图所示,设|PF1|=t,|PF2|=n,
由角平分线的性质可得
| t |
| n |
| |MF1| |
| |F2M| |
m+
| ||
|
又t+n=2a=4,消去t得到
| 4-n |
| n |
| ||
|
2(
| ||
|
∵a-c<n<a+c,即2-
| 3 |
| 3 |
| 3 |
2(
| ||
|
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
∴m的取值范围;(-
| 3 |
| 2 |
| 3 |
| 2 |
(3)证明:设P(x0,y0),
不妨设y0>0,由椭圆方程
| x2 |
| 4 |
取y=
1-
|
-
| ||||
2
|
| x | ||||
4
|
∴k=kl=-
| x0 | ||||||
4
|
| x0 |
| 4y0 |
∵k1=
| y0 | ||
x0+
|
| y0 | ||
x0-
|
∴
| 1 |
| k1 |
| 1 |
| k2 |
| 2x0 |
| y0 |
∴
| 1 |
| kk1 |
| 1 |
| kk2 |
| 4y0 |
| x0 |
| 2x0 |
| y0 |
点评:本题综合考查了椭圆的定义、标准方程及其性质、角平分线的性质、利用导数的几何意义研究切线、斜率计算公式等基础知识,考查了推理能力、分类讨论的思想方法、计算能力、分析问题和解决问题的能力.

练习册系列答案
相关题目
 (2013•江西)椭圆C:
(2013•江西)椭圆C: