题目内容
(本小题满分14分)
如图8,在直角梯形 中,
中, ,
, ,且
,且 .现以
.现以 为一边向形外作正方形
为一边向形外作正方形 ,然后沿边
,然后沿边 将正方形
将正方形 翻折,使平面
翻折,使平面 与平面
与平面 互相垂直,如图9.
互相垂直,如图9.
(1)求证:平面 平面
平面 ;
;
(2)求平面 与平面
与平面 所成锐二面角的大小.
所成锐二面角的大小.
如图8,在直角梯形
 中,
中, ,
, ,且
,且 .现以
.现以 为一边向形外作正方形
为一边向形外作正方形 ,然后沿边
,然后沿边 将正方形
将正方形 翻折,使平面
翻折,使平面 与平面
与平面 互相垂直,如图9.
互相垂直,如图9.(1)求证:平面
 平面
平面 ;
;(2)求平面
 与平面
与平面 所成锐二面角的大小.
所成锐二面角的大小.
证明(1)(法一)因为平面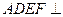 平面
平面 ,
,
且平面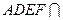 平面
平面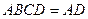 ,
,
又在正方形 中,
中,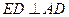 ,
,
所以,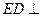 平面
平面 . ………………2分
. ………………2分
而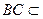 平面
平面 ,
,
所以,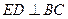 . ………………3分
. ………………3分
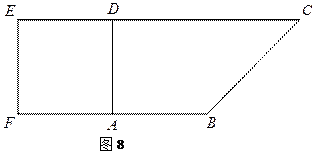
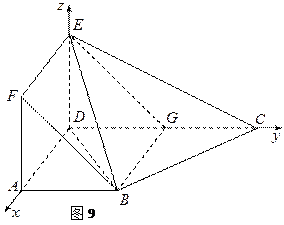
在直角梯形 中,
中, 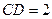 ,
,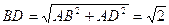 ,
,
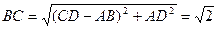 ,
,
所以,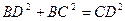 ,
,
所以,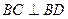 . ………………4分
. ………………4分
又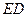 ,
,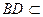 平面
平面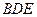 ,
,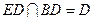 ,
,
所以,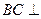 平面
平面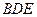 . ………………6分
. ………………6分
而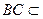 平面
平面 ,
,
所以,平面 平面
平面 . ……………7分
. ……………7分
(法二)同法一,得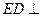 平面
平面 . …………………………2分
. …………………………2分
以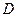 为原点,
为原点,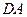 ,
,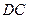 ,
, 分别为
分别为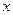 ,
,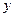
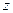 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.
则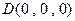 ,
,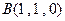 ,
,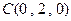 ,
,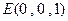 . …………………………3分
. …………………………3分
所以,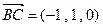 ,
, 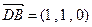 ,
,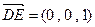 ,
,
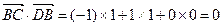 ,
,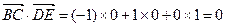 ,
,
所以, ,
,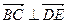 . …………………………………5分
. …………………………………5分
又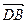 ,
,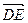 不共线,
不共线,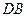 ,
,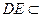 平面
平面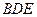 ,
,
所以,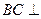 平面
平面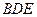 . …………………………6分
. …………………………6分
而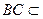 平面
平面 ,
,
所以,平面 平面
平面 . …………………………7分
. …………………………7分
(2)(法一)因为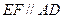 ,
,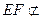 平面
平面 ,
,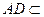 平面
平面 ,
,
所以,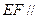 平面
平面 . …………………………9分
. …………………………9分
因为平面 与平面
与平面 有公共点
有公共点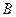 ,
,
所以可设平面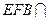 平面
平面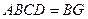 ,
, .
.
因为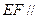 平面
平面 ,
,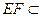 平面
平面 ,平面
,平面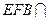 平面
平面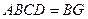 ,
,
所以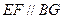 . ………………………10分
. ………………………10分
从而,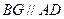 ,
,
又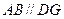 ,且
,且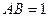 ,
,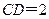 ,所以
,所以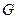 为
为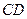 中点,
中点,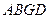 也为正方形. 12分
也为正方形. 12分
易知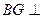 平面
平面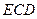 ,所以
,所以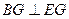 ,
,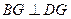 .
.
所以,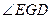 是平面
是平面 与平面
与平面 所成锐二面角的平面角,
所成锐二面角的平面角,
而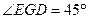 ,
,
所以平面 与平面
与平面 所成锐二面角为
所成锐二面角为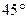 . …………………………14分
. …………………………14分
(法二)由(1)知,平面 的一个法向量是
的一个法向量是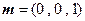 . ………………9分
. ………………9分
设平面 的一个法向量为
的一个法向量为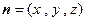 ,
,
因为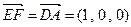 ,
,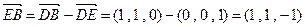
所以,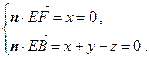 取
取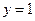 ,得
,得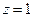 ,所以
,所以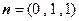 .………………11分
.………………11分
设平面 与平面
与平面 所成锐二面角为
所成锐二面角为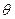 ,
,
则 . ………………………………13分
. ………………………………13分
所以平面 与平面
与平面 所成锐二面角为
所成锐二面角为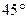 . …………………………14分
. …………………………14分
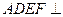 平面
平面 ,
,且平面
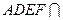 平面
平面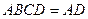 ,
,又在正方形
 中,
中,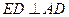 ,
,所以,
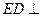 平面
平面 . ………………2分
. ………………2分而
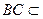 平面
平面 ,
,所以,
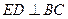 . ………………3分
. ………………3分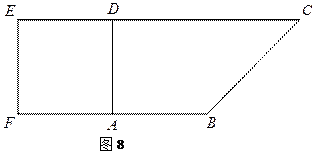
在直角梯形
 中,
中, 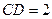 ,
,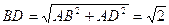 ,
, 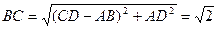 ,
,所以,
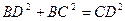 ,
,所以,
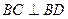 . ………………4分
. ………………4分又
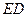 ,
,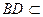 平面
平面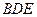 ,
,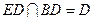 ,
,所以,
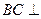 平面
平面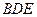 . ………………6分
. ………………6分而
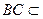 平面
平面 ,
,所以,平面
 平面
平面 . ……………7分
. ……………7分(法二)同法一,得
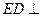 平面
平面 . …………………………2分
. …………………………2分以
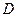 为原点,
为原点,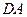 ,
,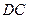 ,
, 分别为
分别为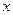 ,
,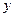
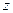 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.则
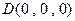 ,
,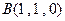 ,
,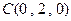 ,
,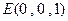 . …………………………3分
. …………………………3分所以,
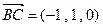 ,
, 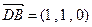 ,
,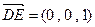 ,
,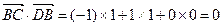 ,
,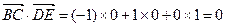 ,
,所以,
 ,
,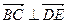 . …………………………………5分
. …………………………………5分又
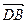 ,
,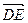 不共线,
不共线,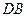 ,
,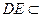 平面
平面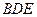 ,
,所以,
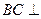 平面
平面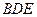 . …………………………6分
. …………………………6分而
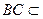 平面
平面 ,
,所以,平面
 平面
平面 . …………………………7分
. …………………………7分(2)(法一)因为
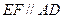 ,
,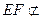 平面
平面 ,
,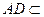 平面
平面 ,
,所以,
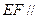 平面
平面 . …………………………9分
. …………………………9分因为平面
 与平面
与平面 有公共点
有公共点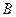 ,
,所以可设平面
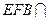 平面
平面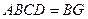 ,
, .
.因为
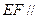 平面
平面 ,
,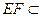 平面
平面 ,平面
,平面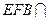 平面
平面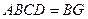 ,
,所以
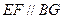 . ………………………10分
. ………………………10分从而,
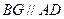 ,
,又
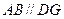 ,且
,且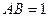 ,
,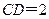 ,所以
,所以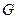 为
为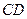 中点,
中点,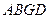 也为正方形. 12分
也为正方形. 12分易知
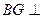 平面
平面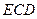 ,所以
,所以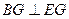 ,
,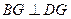 .
.所以,
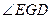 是平面
是平面 与平面
与平面 所成锐二面角的平面角,
所成锐二面角的平面角,而
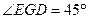 ,
,所以平面
 与平面
与平面 所成锐二面角为
所成锐二面角为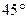 . …………………………14分
. …………………………14分(法二)由(1)知,平面
 的一个法向量是
的一个法向量是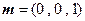 . ………………9分
. ………………9分设平面
 的一个法向量为
的一个法向量为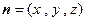 ,
,因为
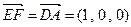 ,
,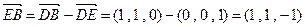
所以,
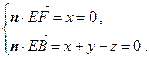 取
取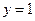 ,得
,得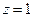 ,所以
,所以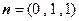 .………………11分
.………………11分设平面
 与平面
与平面 所成锐二面角为
所成锐二面角为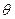 ,
,则
 . ………………………………13分
. ………………………………13分所以平面
 与平面
与平面 所成锐二面角为
所成锐二面角为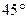 . …………………………14分
. …………………………14分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
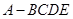 中,
中,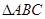 是正三角形,四边形
是正三角形,四边形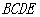 是矩形,且平面
是矩形,且平面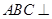 平面
平面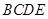 ,
,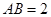 ,
,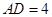 .
.
 是
是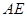 的中点,求证:
的中点,求证: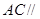 平面
平面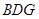 ;
; 为线段
为线段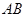 的中点,求二面角
的中点,求二面角 的正切值.
的正切值.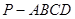 中,
中,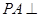 面
面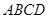 ,
,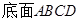 为菱形,且有
为菱形,且有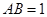 ,
,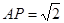 ,∠
,∠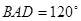 ,
,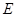 为
为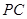 中点.
中点.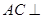 面
面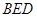 ;
;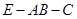 的平面角的余弦值.
的平面角的余弦值.
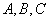 三点不共线,
三点不共线,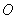 为平面
为平面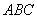 外任一点,若由
外任一点,若由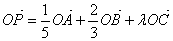 确定的一点
确定的一点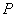 与三点
与三点 .
. 是边长为2的等边三角形,
是边长为2的等边三角形, 平面
平面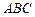 ,
,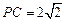 ,
,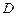 是
是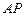 上一动点.
上一动点.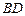 与平面
与平面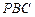 所成的角的正弦值;
所成的角的正弦值;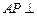 平面
平面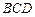 ?请说明理
?请说明理 由.
由.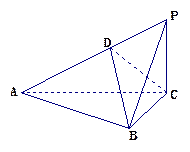
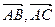 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S; 分别与向量
分别与向量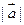 =
=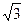 ,求向量
,求向量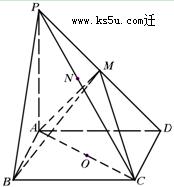
 中,若
中,若 则
则 ( )
( )


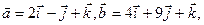 ,则这两个向量的位置关系是___________。
,则这两个向量的位置关系是___________。