题目内容
如图,四棱锥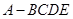 中,
中,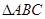 是正三角形,四边形
是正三角形,四边形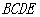 是矩形,且平面
是矩形,且平面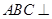 平面
平面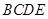 ,
,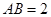 ,
,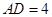 .
.

(Ⅰ) 若点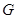 是
是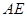 的中点,求证:
的中点,求证: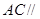 平面
平面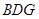 ;
;
(II)若点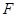 为线段
为线段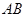 的中点,求二面角
的中点,求二面角 的正切值.
的正切值.
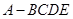 中,
中,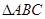 是正三角形,四边形
是正三角形,四边形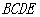 是矩形,且平面
是矩形,且平面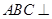 平面
平面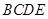 ,
,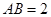 ,
,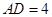 .
.
(Ⅰ) 若点
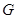 是
是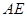 的中点,求证:
的中点,求证: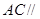 平面
平面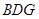 ;
;(II)若点
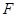 为线段
为线段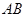 的中点,求二面角
的中点,求二面角 的正切值.
的正切值.(Ⅰ)证明:设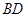 ,
, 交于点
交于点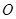 ,连接
,连接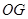 ,易知
,易知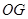 为
为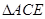 的中位线,
的中位线,
故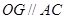 ,又
,又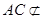 平面
平面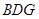 ,
,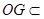 平面
平面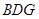 ,得
,得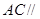 平面
平面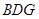 .
.
(Ⅱ)解:过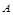 做
做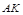

 交
交 于
于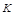 ,过
,过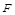 作
作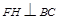 交
交 于
于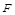 ,
,
由已知可知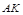
 平面
平面 ,
,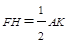 ,且
,且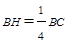 ,
,
过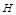 作
作 交
交 于
于 ,连接
,连接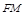 ,由三垂线定理可知:
,由三垂线定理可知: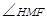 为所求角
为所求角
如图,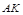
 平面
平面 ,
,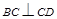 ,由三垂线定理可知,
,由三垂线定理可知,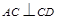
在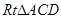 中,斜边
中,斜边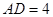 ,
,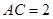 ,得
,得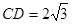 ,
,
在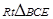 中,
中,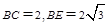 ,得
,得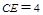 ,由等面积原理得,B到CE边的高为
,由等面积原理得,B到CE边的高为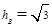
则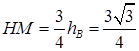 ; 在
; 在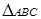 中,
中,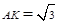 ,则
,则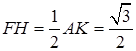 ,
,
故: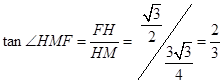
法2建立如图所示的空间直角坐标系,
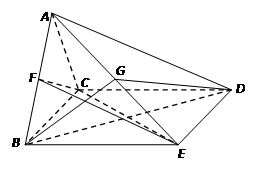
则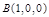 ,
,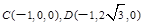 ,
,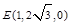 ;
;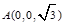 ,
,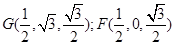
(I)设平面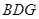 的法向量为
的法向量为 ,
,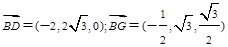
则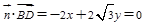 即
即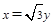 ;推出
;推出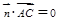 即
即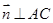 ,
, 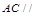 平面
平面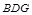 。
。
(II)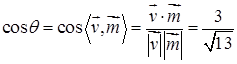 ,故
,故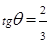
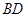 ,
, 交于点
交于点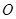 ,连接
,连接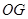 ,易知
,易知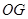 为
为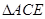 的中位线,
的中位线,故
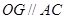 ,又
,又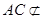 平面
平面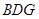 ,
,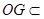 平面
平面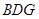 ,得
,得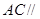 平面
平面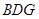 .
.(Ⅱ)解:过
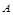 做
做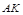

 交
交 于
于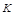 ,过
,过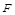 作
作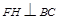 交
交 于
于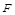 ,
,由已知可知
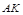
 平面
平面 ,
,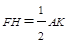 ,且
,且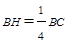 ,
,过
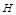 作
作 交
交 于
于 ,连接
,连接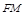 ,由三垂线定理可知:
,由三垂线定理可知: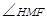 为所求角
为所求角如图,
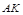
 平面
平面 ,
,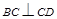 ,由三垂线定理可知,
,由三垂线定理可知,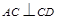
在
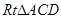 中,斜边
中,斜边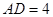 ,
,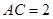 ,得
,得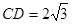 ,
,在
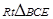 中,
中,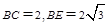 ,得
,得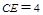 ,由等面积原理得,B到CE边的高为
,由等面积原理得,B到CE边的高为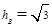
则
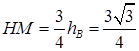 ; 在
; 在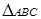 中,
中,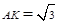 ,则
,则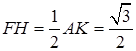 ,
,故:
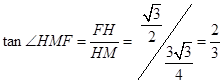
法2建立如图所示的空间直角坐标系,
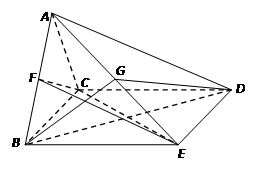
则
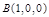 ,
,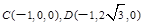 ,
,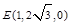 ;
;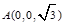 ,
,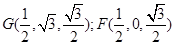
(I)设平面
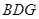 的法向量为
的法向量为 ,
,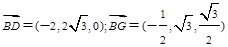
则
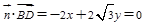 即
即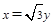 ;推出
;推出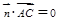 即
即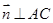 ,
, 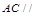 平面
平面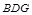 。
。(II)
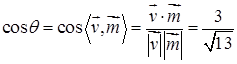 ,故
,故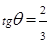
试题分析:建立如图所示的空间直角坐标系,
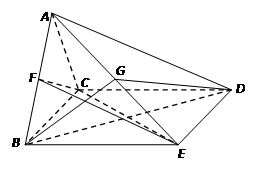
则
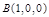 ,
,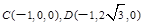 ,
,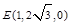 ;
;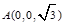 ,
,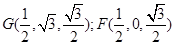
(I)设平面
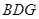 的法向量为
的法向量为 ,
,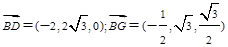
则
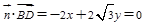 即
即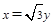 ;
;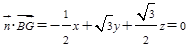 即
即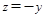
令
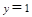 ,则
,则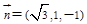 ;又
;又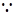
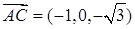 ,故
,故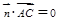 即
即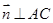 ,而
,而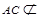 平面
平面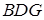 所以
所以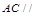 平面
平面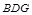 。
。(II)设平面
 的法向量为
的法向量为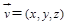 ,
,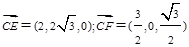 ,
,则
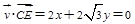 即
即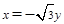 ;
;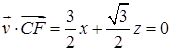 即
即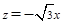
令
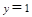 ,则
,则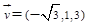 ;由题可知平面
;由题可知平面 的法向量为
的法向量为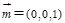
故
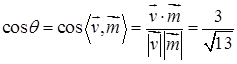 ,故
,故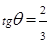
点评:中档题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用空间向量,省去繁琐的证明,也是解决立体几何问题的一个基本思路。对计算能力要求较高。

练习册系列答案
相关题目
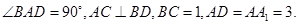
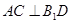 ;
; 所成角的正弦值。
所成角的正弦值。 ,
,

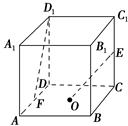




 为正三角形,
为正三角形, ,
, ,AC与BD交于O点.将
,AC与BD交于O点.将 沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为
沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为 ,且P点在平面ABCD内的射影落在
,且P点在平面ABCD内的射影落在
 平面PBD;
平面PBD; 时,求二面角
时,求二面角 的余弦值。
的余弦值。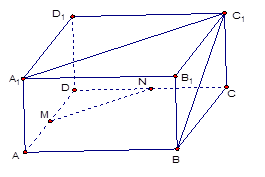
 中,
中, ,
, ,且
,且 .现以
.现以 为一边向形外作正方形
为一边向形外作正方形 ,然后沿边
,然后沿边 平面
平面 ;
; 所成锐二面角的大小.
所成锐二面角的大小.