题目内容
已知向量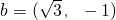 ,|
,| |=2,则|2
|=2,则|2 -
- |的最大值为________.
|的最大值为________.
6
分析:由题意先求出 的模,再利用数量积运算求出
的模,再利用数量积运算求出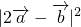 的式子,则当
的式子,则当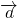
 最小时,所求的模取到最大值,即当cos
最小时,所求的模取到最大值,即当cos =-1时,代入求出所求向量的最大模.
=-1时,代入求出所求向量的最大模.
解答:∵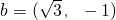 ,∴|
,∴| |=
|= =2,
=2,
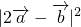 =4
=4 +
+ -4
-4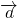
 =16+4-4
=16+4-4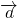
 =20-4
=20-4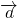
 ,
,
∵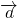
 =4cos
=4cos ,
,
∴当cos =-1时,
=-1时,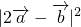 有最大值为36,
有最大值为36,
故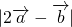 的最大值为6.
的最大值为6.
故答案为:6.
点评:本题考查了向量模的求法,即利用向量的数量积运算 =
= ,此题还利用了三角函数的值域求最大值.
,此题还利用了三角函数的值域求最大值.
分析:由题意先求出
 的模,再利用数量积运算求出
的模,再利用数量积运算求出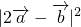 的式子,则当
的式子,则当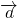
 最小时,所求的模取到最大值,即当cos
最小时,所求的模取到最大值,即当cos =-1时,代入求出所求向量的最大模.
=-1时,代入求出所求向量的最大模.解答:∵
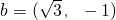 ,∴|
,∴| |=
|= =2,
=2,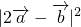 =4
=4 +
+ -4
-4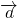
 =16+4-4
=16+4-4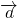
 =20-4
=20-4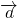
 ,
,∵
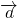
 =4cos
=4cos ,
,∴当cos
 =-1时,
=-1时,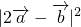 有最大值为36,
有最大值为36,故
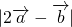 的最大值为6.
的最大值为6.故答案为:6.
点评:本题考查了向量模的求法,即利用向量的数量积运算
 =
= ,此题还利用了三角函数的值域求最大值.
,此题还利用了三角函数的值域求最大值. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目