题目内容

（2012•宜宾一模）设向量|
a
|=
5
x，|
b
|=
2
，且
a
与
b
的夹角为
2
3
π，若f（x）=（
a
+
b
）•（
a
-λ
b
）≤
10
2
（λ-1）x在区间[
2
2
，
2
]上恒成立，则实数λ的取值范围是（　　）
分析：利用向量的数量积公式，再利用分离参数法，确定相应函数的最值，即可求实数λ的取值范围．
解答：解：由题意，∵|
a
|=
5
x，|
b
|=
2
，且
a
与
b
的夹角为
2
3
π，
∴f（x）=（
a
+
b
）•（
a
-λ
b
）=5x2-2λ+（1-λ）×
5
x×
2
×cos
2
3
π
∴不等式等价于5x2-2λ+（1-λ）×
5
x×
2
×cos
2
3
π≤
10
2
（λ-1）x在区间[
2
2
，
2
]上恒成立，
∴5x2-2λ≤0在区间[
2
2
，
2
]上恒成立，
∴λ≥
5
2
x2在区间[
2
2
，
2
]上恒成立
∵函数y=
5
2
x2在区间[
2
2
，
2
]上的最大值为5
∴λ≥5
故选D．
点评：本题考查向量的数量积，考查恒成立问题，解题的关键是分离参数，确定相应函数的最值，属于中档题．
练习册系列答案
相关题目
（2012•宜宾一模）平面α外有两条直线m和n，如果m和n在平面α内的射影分别是m1和n1，给出下列四个命题：
①m1⊥n1⇒m⊥n；
②m⊥n⇒m1⊥n1
③m1与n1相交⇒m与n相交或重合
④m1与n1平行⇒m与n平行或重合
其中不正确的命题个数是（　　）
（2012•宜宾一模）已知向量
a
=（2，l），
a
•
b
=10，|
a
+
b
|=5
2
，则|
b
|=
5
5
．
（2012•宜宾一模）已知向量
a
=(1，2)，向量
b
=(x，-2)，且
a
⊥(
a
-
b
)，则实数x等于
9
9
．
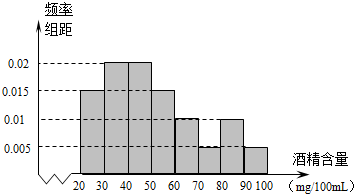（2012•宜宾一模）《中华人民共和国道路交通安全法》
规定：车辆驾驶员血液酒精浓度在20～80mg/100mL（不含80）之间，属于酒后驾车；血液酒精浓度在80mg/100mL（含80）以上时，属醉酒驾车．
据有关调查，在一周内，某地区查处酒后驾车和醉酒驾车共500人．如图是对这500人血液中酒精含量进行检测所得结果的频率分布直方图，则属于醉酒驾车的人数约为
75
75
．
（2012•宜宾一模）若a＞b，则下列不等式正确的是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网