题目内容
（2012•宜宾一模）已知向量
=(1，2)，向量
=(x，-2)，且
⊥(
-
)，则实数x等于
| a |
| b |
| a |
| a |
| b |
9
9
．分析：利用两个向量共线，它们的坐标满足x1y2-x2y1=0，解方程求得x的值．
解答：解：∵向量
=(1，2)，向量
=(x，-2)，
∴
-
=（1-x，4）．
∴
⊥(
-
)，
∴
•(
-
)=（1，2）•（1-x，4）=1-x+8=0，
∴x=9，
故答案为 9．
| a |
| b |
∴
| a |
| b |
∴
| a |
| a |
| b |
∴
| a |
| a |
| b |
∴x=9，
故答案为 9．
点评：本题主要考查两个向量垂直的性质，两个向量坐标形式的运算，属于基础题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
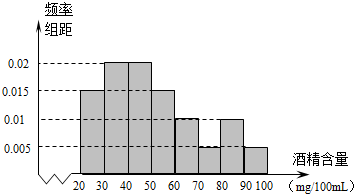（2012•宜宾一模）《中华人民共和国道路交通安全法》