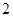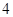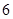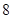题目内容
若抛物线 的焦点与椭圆
的焦点与椭圆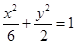 的右焦点重合,则p的值为( )
的右焦点重合,则p的值为( )
| A.-2 | B.2 | C.-4 | D.4 |
D
解析试题分析:先根据椭圆方程求出椭圆的右交点坐标,因为抛物线y2=2px的焦点与椭圆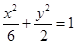 的右焦点重合,所以抛物线的焦点坐标可知,再根据抛物线中焦点坐标为(
的右焦点重合,所以抛物线的焦点坐标可知,再根据抛物线中焦点坐标为(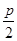 ,0),即可求出p值,由题,a2=2,b2=2,∴c2=4,c=2,∵抛物线y2=2px的焦点与椭圆
,0),即可求出p值,由题,a2=2,b2=2,∴c2=4,c=2,∵抛物线y2=2px的焦点与椭圆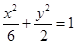 的右焦点重合,∴抛物线y2=2px中p=4,选D.
的右焦点重合,∴抛物线y2=2px中p=4,选D.
考点:椭圆的简单性质和抛物线的简单性质.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
抛物线 的准线方程是 ( )
的准线方程是 ( )
A. | B.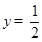 | C. | D. |
已知双曲线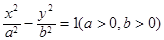 的两条渐近线均与圆
的两条渐近线均与圆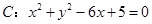 相切,则该双曲线离心率等于
相切,则该双曲线离心率等于
A.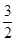 | B.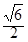 | C.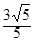 | D.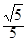 |
椭圆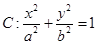
 的左、右焦点分别为
的左、右焦点分别为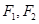 ,
,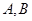 是
是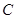 上两点,
上两点,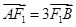 ,
, ,则椭圆
,则椭圆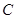 的离心率为( )
的离心率为( )
A.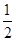 | B.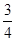 | C.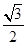 | D.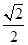 |
已知直线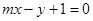 交抛物线
交抛物线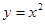 于
于 、
、 两点,则△
两点,则△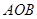 ( )
( )
| A.为直角三角形 | B.为锐角三角形 |
| C.为钝角三角形 | D.前三种形状都有可能 |
椭圆 的焦距为( )
的焦距为( )
| A.10 | B.5 | C. | D. |
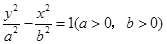 的离心率为2,若抛物线C2:
的离心率为2,若抛物线C2: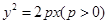 的焦点到双曲线C1的渐近线的距离是2,则抛物线C2的方程是
的焦点到双曲线C1的渐近线的距离是2,则抛物线C2的方程是
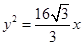
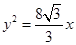

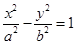 (
(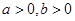 )的左、右焦点分别是
)的左、右焦点分别是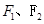 ,过
,过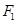 作倾斜角为
作倾斜角为 的直线交双曲线右支于
的直线交双曲线右支于 点,若
点,若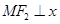 轴,则双曲线的离心率为( )
轴,则双曲线的离心率为( )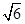
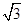
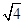
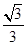
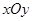 中,抛物线
中,抛物线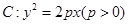 的焦点为
的焦点为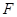 ,
,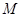 是抛物线
是抛物线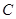 上的点,若
上的点,若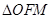 的外接圆与抛物线
的外接圆与抛物线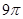 ,则
,则 ( )
( )