题目内容
5.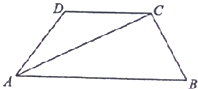 如图,在梯形ABCD中,AB∥CD,且AB=2CD,设$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.
如图,在梯形ABCD中,AB∥CD,且AB=2CD,设$\overrightarrow{AD}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$.(1)试用$\overrightarrow{a}$和$\overrightarrow{b}$表示$\overrightarrow{AC}$;
(2)若点P满足$\overrightarrow{AP}$=$\frac{3}{4}\overrightarrow{a}$+λ$\overrightarrow{b}$,且B,D,P三点共线,求实数λ的值.
分析 (1)利用向量三角形法则可得:$\overrightarrow{DC}=\overrightarrow{AC}-\overrightarrow{AD}$,$\overrightarrow{AB}=\overrightarrow{CB}-\overrightarrow{CA}$,$\overrightarrow{AB}=2\overrightarrow{DC}$,化简整理即可得出.
(2)由B,D,P三点共线,可得存在实数k使得$\overrightarrow{AP}=k\overrightarrow{AB}+(1-k)\overrightarrow{AD}$.又$\overrightarrow{DC}=\overrightarrow{AC}-\overrightarrow{AD}$,$\overrightarrow{AB}=2\overrightarrow{DC}$,可得$\overrightarrow{AC}=\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$,又$\overrightarrow{AP}$=$\frac{3}{4}\overrightarrow{AD}+λ\overrightarrow{BC}$=$\frac{3}{4}\overrightarrow{AD}$+λ$(\overrightarrow{AC}-\overrightarrow{AB})$.可得$\overrightarrow{AP}$=$-\frac{3}{2}\overrightarrow{AB}$+$(\frac{3}{4}+λ)\overrightarrow{AD}$.再利用向量基本定理即可得出.
解答 解:(1)∵$\overrightarrow{DC}=\overrightarrow{AC}-\overrightarrow{AD}$,$\overrightarrow{AB}=\overrightarrow{CB}-\overrightarrow{CA}$,$\overrightarrow{AB}=2\overrightarrow{DC}$,
∴存在实数k满足:$\overrightarrow{CB}-\overrightarrow{CA}$=2$(\overrightarrow{AC}-\overrightarrow{AD})$,
化为$\overrightarrow{AC}$=$\frac{1}{3}$$\overrightarrow{BC}$+$\frac{2}{3}$$\overrightarrow{AD}$=$\frac{1}{3}\overrightarrow{b}$+$\frac{2}{3}\overrightarrow{a}$.
(2)∵B,D,P三点共线,
∴$\overrightarrow{AP}=k\overrightarrow{AB}+(1-k)\overrightarrow{AD}$.
∵$\overrightarrow{DC}=\overrightarrow{AC}-\overrightarrow{AD}$,$\overrightarrow{AB}=2\overrightarrow{DC}$,
∴$\overrightarrow{AC}=\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$,
又$\overrightarrow{AP}$=$\frac{3}{4}\overrightarrow{a}$+λ$\overrightarrow{b}$=$\frac{3}{4}\overrightarrow{AD}+λ\overrightarrow{BC}$=$\frac{3}{4}\overrightarrow{AD}$+λ$(\overrightarrow{AC}-\overrightarrow{AB})$.
∴$\overrightarrow{AP}$=$\frac{3}{4}\overrightarrow{AD}$+λ$(\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB})$-$λ\overrightarrow{AB}$=$-\frac{3}{2}\overrightarrow{AB}$+$(\frac{3}{4}+λ)\overrightarrow{AD}$.
∴$\left\{\begin{array}{l}{-\frac{3}{2}=k}\\{\frac{3}{4}+λ=1-k}\end{array}\right.$,解得$k=-\frac{3}{2}$,λ=$\frac{7}{4}$.
∴λ=$\frac{7}{4}$.
点评 本题考查了向量数量积运算性质、向量共线定理、向量基本定理、三角形法则,考查了推理能力与计算能力,属于中档题.

| A. | -1 | B. | 0 | C. | 1 | D. | -2 |
| A. | $\frac{8}{9}$ | B. | -$\frac{1}{9}$ | C. | $\frac{4}{3}$ | D. | $\frac{1}{3}$ |
| A. | P(X=i)=0.1,i=0,1,2,3,4 | B. | P(X=i)=$\frac{{i}^{2}+5}{50}$,i=1,2,3,4,5 | ||
| C. | P(X=i)=$\frac{i}{10}$,i=1,2,3,4,5 | D. | P(X=i)=0.2,i=1,2,3,4,5 |