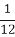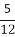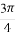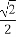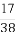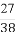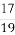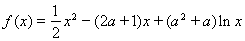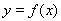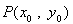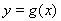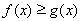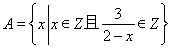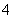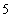题目内容
一个袋中装有若干个大小相同的黑球、白球和红球,已知从袋中任意摸出1个球,得到黑球的概率是 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是 .
.
(1)若袋中共有10个球,
①求白球的个数;
②从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的分布列.
(2)求证:从袋中任意摸出2个球,至少得到1个黑球的概率不大于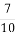 ,并指出袋中哪种颜色的球的个数最少.
,并指出袋中哪种颜色的球的个数最少.
(1) ①5 ②X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
(2)见解析
【解析】(1)①记“从袋中任意摸出2个球,至少得到1个白球”为事件A,设袋中白球的个数为x,则
P(A)=1-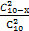 =
=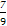 ,得x=5或x=14(舍去).故白球有5个.
,得x=5或x=14(舍去).故白球有5个.
②随机变量X的取值为0,1,2,3,
P(X=0)=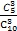 =
=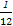 ;P(X=1)=
;P(X=1)=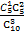 =
=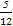 ;
;
P(X=2)=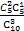 =
=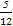 ;P(X=3)=
;P(X=3)=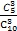 =
=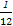 .
.
故X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
(2)设袋中有n个球,其中有y个黑球,
由题意得y=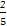 n,所以2y<n,2y≤n-1,故
n,所以2y<n,2y≤n-1,故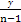 ≤
≤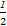 .
.
记“从袋中任意摸出2个球,至少有1个黑球”为事件B,
则P(B)=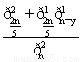
=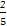 ·
·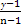 +
+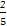 ·
·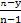 +
+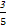 ·
·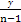
=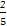 +
+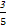 ×
×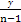 ≤
≤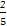 +
+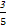 ×
×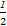 =
= .
.
所以白球的个数比黑球多,白球个数多于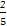 n,红球的个数少于
n,红球的个数少于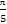 ,故袋中红球个数最少.
,故袋中红球个数最少.
【方法技巧】随机变量分布列的求法
(1)搞清随机变量每个取值对应的随机事件,思考目标事件如何用基本事件来表示,求出随机变量所有可能的值.
(2)利用对立事件和互斥事件求出取每一个值时的概率,计算必须准确无误.
(3)注意运用分布列的两条性质检验所求概率,确保正确后列出分布列.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目