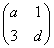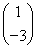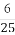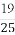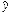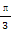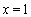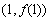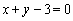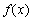题目内容
已知曲线C:ρsin(θ+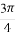 )=
)=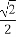 ,曲线P:ρ2-4ρcosθ+3=0,
,曲线P:ρ2-4ρcosθ+3=0,
(1)求曲线C,P的直角坐标方程.
(2)设曲线C和曲线P的交点为A,B,求|AB|.
(1) x2+y2-4x+3=0 (2) 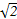
【解析】(1)由ρsin(θ+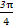 )=
)= ,得
,得
ρ[sinθ·(- )+cosθ·
)+cosθ· ]=
]= ,
,
∴ρcosθ-ρsinθ-1=0,
∴x-y-1=0,
由ρ2-4ρcosθ+3=0,
得x2+y2-4x+3=0.
(2)曲线P表示为(x-2)2+y2=1表示圆心在(2,0),半径r=1的圆,
由于圆心到直线C的距离为d=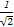 =
= ,
,
∴|AB|=2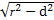 =
=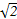 .
.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目