题目内容
(本小题满分12分)设函数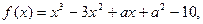 若它是R上的单调函数,且1是它的零点。
若它是R上的单调函数,且1是它的零点。
(1)求实数a的值;
(2)设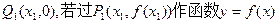 的图象的切线与x轴交于点
的图象的切线与x轴交于点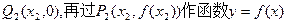 的图象的切线与x轴于
的图象的切线与x轴于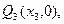 ……,依此下去,过
……,依此下去,过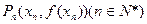 作函数
作函数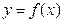 的图象的切线与x轴交于点
的图象的切线与x轴交于点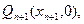 ……,若
……,若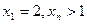 求证:
求证: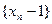 成等比数列;并求数列
成等比数列;并求数列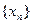 的通项公式
的通项公式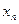 。(已知
。(已知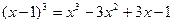 )
)
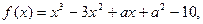 若它是R上的单调函数,且1是它的零点。
若它是R上的单调函数,且1是它的零点。(1)求实数a的值;
|
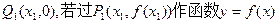 的图象的切线与x轴交于点
的图象的切线与x轴交于点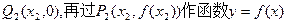 的图象的切线与x轴于
的图象的切线与x轴于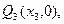 ……,依此下去,过
……,依此下去,过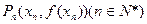 作函数
作函数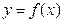 的图象的切线与x轴交于点
的图象的切线与x轴交于点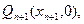 ……,若
……,若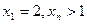 求证:
求证: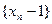 成等比数列;并求数列
成等比数列;并求数列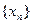 的通项公式
的通项公式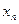 。(已知
。(已知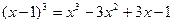 )
) (1)3(2)见解析
(1)由1是函数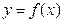 的零点:
的零点:
得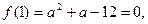
解得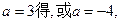 ……………………………………2分
……………………………………2分
若a=3,则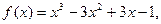
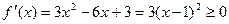 恒成立,满足条件:
恒成立,满足条件:
若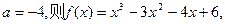
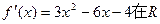 上有正,有负,不满足“是R上的增函数”条件,所以舍去。
上有正,有负,不满足“是R上的增函数”条件,所以舍去。
所以,a=3…………………………6分
(2)由(1)知
过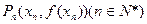 作函数
作函数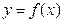 图象的切线方程:
图象的切线方程:
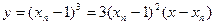 ,……………………8分
,……………………8分
令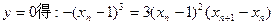 ,
,
∵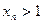
∴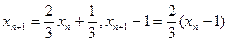
∴数列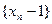 是以1为首项,
是以1为首项,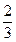 为公比的等比数列………………10分
为公比的等比数列………………10分
∴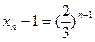
∴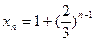 ……………………12分
……………………12分
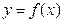 的零点:
的零点:得
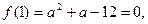
解得
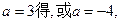 ……………………………………2分
……………………………………2分若a=3,则
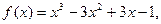
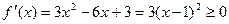 恒成立,满足条件:
恒成立,满足条件:若
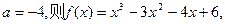
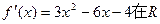 上有正,有负,不满足“是R上的增函数”条件,所以舍去。
上有正,有负,不满足“是R上的增函数”条件,所以舍去。所以,a=3…………………………6分
(2)由(1)知

过
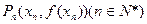 作函数
作函数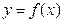 图象的切线方程:
图象的切线方程: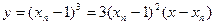 ,……………………8分
,……………………8分令
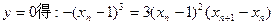 ,
,∵
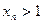
∴
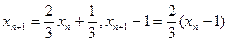
∴数列
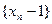 是以1为首项,
是以1为首项,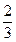 为公比的等比数列………………10分
为公比的等比数列………………10分∴
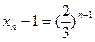
∴
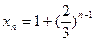 ……………………12分
……………………12分
练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目

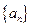 中
中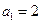 ,
,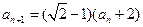 ,
,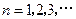 .
.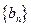 中
中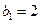 ,
,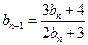 ,
,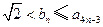 ,
,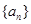 满足
满足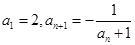 ,则
,则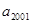 等于( )
等于( )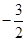
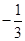
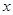 ,以后每次生成的结果是将上一次生成的每一个数
,以后每次生成的结果是将上一次生成的每一个数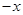 ,另一个是
,另一个是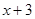 .设第
.设第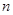 次生成的数的个数为
次生成的数的个数为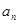 ,
,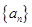 的前
的前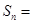 ;若
;若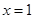 ,前
,前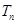 ,则
,则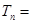 .
.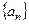 的前
的前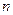 项和
项和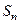 满足
满足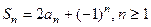 .
.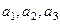 ;
;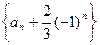 为等比数列,并求出
为等比数列,并求出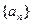 满足
满足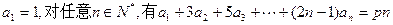 (p为常数)
(p为常数)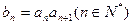 ,求数列
,求数列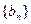 的前n项和
的前n项和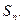
 为等差数列,
为等差数列, 为其前
为其前 项和
项和
 的反函数为
的反函数为 ,则
,则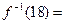 。
。 平面ABC,AB
平面ABC,AB BC,DA=AB=BC=
BC,DA=AB=BC= ,则球O的体积等于 。
,则球O的体积等于 。 (
( ,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的
,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的 ,则此次数学考试成绩不低于110分的学生约有 人。
,则此次数学考试成绩不低于110分的学生约有 人。
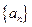 满足
满足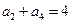 ,
,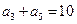 ,则它的前10项的和
,则它的前10项的和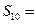 ( )
( )