题目内容
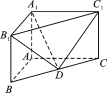
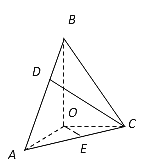
【题目】如图,多面体![]() 是正三棱柱(底面是正三角形的直棱柱)
是正三棱柱(底面是正三角形的直棱柱)![]() 沿平面
沿平面![]() 切除一部分所得,其中平面
切除一部分所得,其中平面![]() 为原正三棱柱的底面,
为原正三棱柱的底面,![]() ,点D为
,点D为![]() 的中点.
的中点.
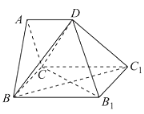
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)设![]() 与
与![]() 交于点E,连接
交于点E,连接![]() 、
、![]() ,由题意可得四边形
,由题意可得四边形![]() 是正方形,且
是正方形,且![]() ,再由点D为
,再由点D为![]() 的中点,
的中点,![]() 平行且等于
平行且等于![]() ,求得CD,同理求得
,求得CD,同理求得![]() ,得
,得![]() ,可得
,可得![]() ,由线面垂直的判定可得;
,由线面垂直的判定可得;
(2)取BC的中点O,连接AO,可得AO⊥BC,由正棱柱的性质可得AO⊥平面![]() ,以O为坐标原点,向量
,以O为坐标原点,向量![]() 、
、![]() 、
、![]() 分别为x、y,z轴建立空间直角坐标系,分别求出平面CBD与平面
分别为x、y,z轴建立空间直角坐标系,分别求出平面CBD与平面![]() 的一个法向量,由两法向量所成角的余弦值可得二面角
的一个法向量,由两法向量所成角的余弦值可得二面角![]() 的平面角的余弦值.
的平面角的余弦值.
(1)设![]() 与
与![]() 交于点E,连接
交于点E,连接![]() 、
、![]() .
.
∵多面体![]() 是正三棱柱沿平面
是正三棱柱沿平面![]() 切除部分所得,
切除部分所得,![]() ,
,
∴四边形![]() 是正方形,且
是正方形,且![]() .
.
∵点D为![]() 的中点,
的中点,![]() 平行且等于
平行且等于![]() ,
,
∴![]() .
.
同理![]() ,
,
∴![]() .
.
∵E为![]() 的中点,
的中点,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ;
;
(2)取![]() 的中点O,连接
的中点O,连接![]() .
.
∵![]() 为正三角形,
为正三角形,![]() .
.
由正棱柱的性质可得,平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
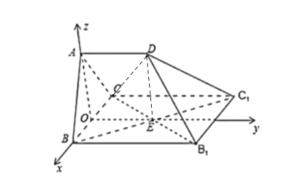
以点O为原点,向量![]() 、
、![]() 、
、![]() 分别为x、y,z轴正方向建立如图所示空间直角坐标系
分别为x、y,z轴正方向建立如图所示空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则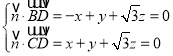 ,
,
令![]() ,得
,得![]() ,
,![]() ,即
,即![]() .
.
由(1)可知,平面![]() 的一个法向量为
的一个法向量为![]() .
.
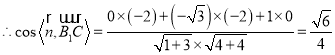 ,
,
又∵二面角![]() 的平面角为锐角,
的平面角为锐角,
∴二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
【题目】某品牌奶茶公司计划在A地开设若干个连锁加盟店,经调查研究,加盟店的个数x与平均每个店的月营业额y(万元)具有如下表所示的数据关系:
x | 2 | 4 | 6 | 8 | 10 |
y | 20.9 | 20.2 | 19 | 17.8 | 17.1 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的结果分析,为了保证平均每个加盟店的月营业额不少于14.6万元,则A地开设加盟店的个数不能超过几个?
参考公式:线性回归方程![]() 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为
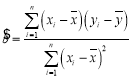 ,
,![]()