Question

设

i

，

j

是平面直角坐标系（坐标原点为0）内分别与x轴、y轴的正方向相同的两个单位向量，且

OA

=-2

i

+

j

，

OB

=4

i

+3

j

，则△OAB的面积为（　　）

• A．

  2 5

  5

• B．5
• C．10
• D．15

Answer 1

分析：根据题意，可得A（-2，1）且B（4，3），利用向量共线的条件解出直线AB交y轴于点C（0，

5

3

），由此结合三角形面积公式加以计算，即可得到△OAB的面积为5．

解答：解：∵

i

，

j

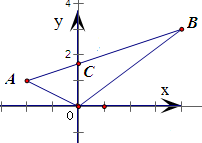是平面直角坐标系与x轴、y轴的正方向相同的两个单位向量，
∴由

OA

=-2

i

+

j

，可得A（-2，1）；由

OB

=4

i

+3

j

，可得B（4，3）
直线AB交y轴于点C，设C（0，k），得

AC

=(2，k-1)，

AB

=(6，2)
∵

AC

、

AB

共线，∴6（k-1）=2×2，解得k=

5

3

，
所以C（0，

5

3

），因此△OAB的面积为
S=

1

2

|OC|•（x_B-x_A）=

1

2

×

5

3

×(4+2)=5
故选：B

点评：本题给出向量

OA

、

OB

的坐标，求△OAB的面积．着重考查了平面向量平行的条件、向量的坐标运算和三角形的面积公式等知识，属于基础题．