题目内容
设函数f(x)=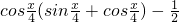
(Ⅰ)求函数y=f(x)取最值时x的取值集合;
(Ⅱ)在△ABC中,角A、B、C的对边分别是a,b,c,且满(2a-c)cosB=bcosC,求函数f(A)的取值范围.
解:(1)∵函数f(x)=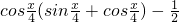 =
= +
+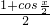 -
- =
= (sin
(sin +cos
+cos )=
)= sin(
sin( +
+ ),…(4分)
),…(4分)
故当 +
+ =kπ+
=kπ+ ,k∈z 时,f(x)取最值,
,k∈z 时,f(x)取最值,
此时x取值的集合:{x|x=kπ+ },k∈z. …(6分)
},k∈z. …(6分)
(2)∵(2a-c)cosB=Bcosc,∴(2sinA-sinC)cosB=sinBcosC,
2sinAcosB=sinCcosB+sinBcosC=sin(B+C)=sinA. …(8分)
∴2conB=1,∴B= .
.
∵f(A)═ sin(
sin(  +
+ ),且 0<A<
),且 0<A< ,
,
∴ <
< +
+ <
< ,
,
∴ <f(A)≤
<f(A)≤ ,故函数f(A)的取值范围为(
,故函数f(A)的取值范围为( ,
, ]. …(12分)
]. …(12分)
分析:(1)利用两角和差的正弦公式化简函数f(x)的解析式为 sin(
sin( +
+ ),哟此求得函数y=f(x)取最值时x的取值集合.
),哟此求得函数y=f(x)取最值时x的取值集合.
(2)根据(2a-c)cosB=Bcosc,利用正弦定理可得 2conB=1,B= . 再由f(A)═
. 再由f(A)═ sin(
sin(  +
+ ),以及 0<A<
),以及 0<A< ,求得函数f(A)的取值范围.
,求得函数f(A)的取值范围.
点评:本题主要考查两角和差的正弦公式、正弦定理的应用,正弦函数的定义域和值域,属于中档题.
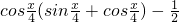 =
= +
+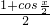 -
- =
= (sin
(sin +cos
+cos )=
)= sin(
sin( +
+ ),…(4分)
),…(4分)故当
 +
+ =kπ+
=kπ+ ,k∈z 时,f(x)取最值,
,k∈z 时,f(x)取最值,此时x取值的集合:{x|x=kπ+
 },k∈z. …(6分)
},k∈z. …(6分)(2)∵(2a-c)cosB=Bcosc,∴(2sinA-sinC)cosB=sinBcosC,
2sinAcosB=sinCcosB+sinBcosC=sin(B+C)=sinA. …(8分)
∴2conB=1,∴B=
 .
.∵f(A)═
 sin(
sin(  +
+ ),且 0<A<
),且 0<A< ,
,∴
 <
< +
+ <
< ,
,∴
 <f(A)≤
<f(A)≤ ,故函数f(A)的取值范围为(
,故函数f(A)的取值范围为( ,
, ]. …(12分)
]. …(12分)分析:(1)利用两角和差的正弦公式化简函数f(x)的解析式为
 sin(
sin( +
+ ),哟此求得函数y=f(x)取最值时x的取值集合.
),哟此求得函数y=f(x)取最值时x的取值集合.(2)根据(2a-c)cosB=Bcosc,利用正弦定理可得 2conB=1,B=
 . 再由f(A)═
. 再由f(A)═ sin(
sin(  +
+ ),以及 0<A<
),以及 0<A< ,求得函数f(A)的取值范围.
,求得函数f(A)的取值范围.点评:本题主要考查两角和差的正弦公式、正弦定理的应用,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 (2012•重庆)设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
(2012•重庆)设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )