题目内容
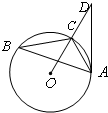如图，已知△ABC内接于⊙O，点D在OC的延长线上，AD切⊙O于A，若∠ABC=30°，AC=2，则AD的长为分析：根据已知可得△AOC是等边三角形，从而得到OA=AC=2，则可以利用勾股定理求得AD的长．
解答：解：（2）∵OA=OC，∠AOC=60°，
∴△AOC是等边三角形，
∴OA=AC=2，
∵∠OAD=90°，∠D=30°，
∴AD=
•AO=2
．
故答案为：2
．
∴△AOC是等边三角形，
∴OA=AC=2，
∵∠OAD=90°，∠D=30°，
∴AD=
| 3 |
| 3 |
故答案为：2
| 3 |
点评：本题考查和圆有关的比例线段，考查同弧所对的圆周角等于弦切角，本题在数据运算中主要应用含有30°角的直角三角形的性质，本题是一个基础题．
练习册系列答案
相关题目
如图，已知△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，DC⊥平面ABC，AB=2，
如图，已知△ABC内接于圆O，AB是圆O的直径，四边形DBCE为平行四边形，EC⊥平面ABC，AB=2AC=2，
如图，已知△ABC内接于圆⊙O，点D在OC的延长线上，AD是⊙O的切线，若∠B=30°，AC=
如图，已知△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，DC⊥平面ABC，AB=2，