题目内容
 如图,已知△ABC内接于圆⊙O,点D在OC的延长线上,AD是⊙O的切线,若∠B=30°,AC=
如图,已知△ABC内接于圆⊙O,点D在OC的延长线上,AD是⊙O的切线,若∠B=30°,AC=| 3 |
分析:做出辅助线,根据同弧所对的圆周角等于圆心角的一半,写出两个角之间的关系,得到顶角是60度的等腰三角形是一个等边三角形,求出OC=AC=
;再结合弦切角定理然后在RT△OAD中求出AD,最后代入三角形的面积公式即可得到结果.
| 3 |
解答:解:连接AO,
则∠AOD=2∠B=60°,
∵OA=OC
∴△AOC是一个等边三角形,
∴OC=AC=
.
∵AD是⊙O的切线
∴∠CAD=∠B=30°.
在RT△OAD中,tan∠DOA=
⇒AD=OA•tan∠DOA=3.
∴S△CAD=
•AC•AD•sin∠CAD=
×
×3×
=
.
故选:D.
则∠AOD=2∠B=60°,

∵OA=OC
∴△AOC是一个等边三角形,
∴OC=AC=
| 3 |
∵AD是⊙O的切线
∴∠CAD=∠B=30°.
在RT△OAD中,tan∠DOA=
| AD |
| OA |
∴S△CAD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
3
| ||
| 4 |
故选:D.
点评:本题考查同弧所对的圆周角和圆心角之间的关系以及弦切角的应用.本题解题的关键是做出辅助线,得到边和角之间的关系.解决这一类型题目的关键是熟练掌握与圆有关的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
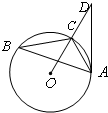 如图,已知△ABC内接于⊙O,点D在OC的延长线上,AD切⊙O于A,若∠ABC=30°,AC=2,则AD的长为
如图,已知△ABC内接于⊙O,点D在OC的延长线上,AD切⊙O于A,若∠ABC=30°,AC=2,则AD的长为 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2, 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DBCE为平行四边形,EC⊥平面ABC,AB=2AC=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DBCE为平行四边形,EC⊥平面ABC,AB=2AC=2, 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,