题目内容
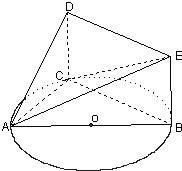 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
| ||
| 2 |
(1)证明:平面ACD⊥平面ADE;
(2)记AC=x,V(x)表示三棱锥A-CBE的体积,求V(x)的表达式.
分析:(1)欲证平面ACD⊥平面ADE,根据面面垂直的判定定理可知在平面ADE内一直线与平面ACD垂直,而根据题意可得DE⊥平面ADC;
(2)要求三棱锥A-CBE的体积,可转化成求出三棱锥E-ABC的体积,而该三棱锥的高为BE易于求解,然后根据三棱锥的体积公式进行求解即可.
(2)要求三棱锥A-CBE的体积,可转化成求出三棱锥E-ABC的体积,而该三棱锥的高为BE易于求解,然后根据三棱锥的体积公式进行求解即可.
解答:解:(1)证明:∵四边形DCBE为平行四边形∴CD∥BE,BC∥DE
∵DC⊥平面ABC,BC?平面ABC∴DC⊥BC.
∵AB是圆O的直径∴BC⊥AC且DC∩AC=C∴BC⊥平面ADC.
∵DE∥BC∴DE⊥平面ADC
又∵DE?平面ADE
∴平面ACD⊥平面ADE
(2)∵DC⊥平面ABC,CD∥BE∴BE⊥平面ABC
∵AB?平面ABC∴BE⊥AB,
在Rt△ABE中,由tan∠EAB=
=
,AB=2得BE=
在Rt△ABC中∵AC=
=
(0<x<2)
∴S△ABC=
AC•BC=
x
∴V(x)=VC-ABE=VE-ABC=
S△ABC•BE=
x
(0<x<2)
∵DC⊥平面ABC,BC?平面ABC∴DC⊥BC.
∵AB是圆O的直径∴BC⊥AC且DC∩AC=C∴BC⊥平面ADC.
∵DE∥BC∴DE⊥平面ADC
又∵DE?平面ADE
∴平面ACD⊥平面ADE
(2)∵DC⊥平面ABC,CD∥BE∴BE⊥平面ABC
∵AB?平面ABC∴BE⊥AB,
在Rt△ABE中,由tan∠EAB=
| BE |
| AB |
| ||
| 2 |
| 3 |
在Rt△ABC中∵AC=
| AB2-BC2 |
| 4-x2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 4-x2 |
∴V(x)=VC-ABE=VE-ABC=
| 1 |
| 3 |
| ||
| 6 |
| 4-x2 |
点评:本题主要考查了平面与平面垂直的判定,以及棱锥的体积和转化的数学思想,属于基础题.

练习册系列答案
相关题目
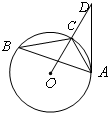 如图,已知△ABC内接于⊙O,点D在OC的延长线上,AD切⊙O于A,若∠ABC=30°,AC=2,则AD的长为
如图,已知△ABC内接于⊙O,点D在OC的延长线上,AD切⊙O于A,若∠ABC=30°,AC=2,则AD的长为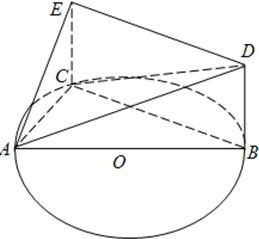 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DBCE为平行四边形,EC⊥平面ABC,AB=2AC=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DBCE为平行四边形,EC⊥平面ABC,AB=2AC=2,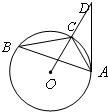 如图,已知△ABC内接于圆⊙O,点D在OC的延长线上,AD是⊙O的切线,若∠B=30°,AC=
如图,已知△ABC内接于圆⊙O,点D在OC的延长线上,AD是⊙O的切线,若∠B=30°,AC=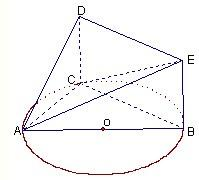 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,