题目内容
 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
| ||
| 2 |
(1)证明:平面ACD⊥平面ADE;
(2)记AC=x,V(x)表示三棱锥A-CBE的体积,求V(x)的表达式;
(3)当V(x)取得最大值时,求证:AD=CE.
分析:(1)由已知,可以证明BC⊥平面ADC,又DE∥BC得出DE⊥平面ADC,根据两个平面垂直的判定定理即可证出平面ACD⊥平面ADE;
(2)注意到VA-CBE=VE-ACB,BE为高,根据勾股定理用x表示出BC,代入锥体体积公式可得V(x)的表达式
(3)在(2)的基础上,利用函数求值域、最值的方法求出x的值后,再去证明AD=CE.
(2)注意到VA-CBE=VE-ACB,BE为高,根据勾股定理用x表示出BC,代入锥体体积公式可得V(x)的表达式
(3)在(2)的基础上,利用函数求值域、最值的方法求出x的值后,再去证明AD=CE.
解答:解:
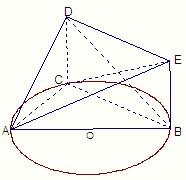
(1)证明:∵四边形DCBE为平行四边形∴CD∥BE,BC∥DE---------(1分)
∵DC⊥平面ABC,BC?平面ABC∴DC⊥BC.----------(2分)
∵AB是圆O的直径∴BC⊥AC且DC∩AC=C
∴BC⊥平面ADC.
∵DE∥BC∴DE⊥平面ADC---------------------------------------(3分)
又∵DE?平面ADE∴平面ACD⊥平面ADE----------------(4分)
(2)∵DC⊥平面ABC,CD∥BE∴BE⊥平面ABC
∵AB?平面ABC∴BE⊥AB,--------------------------------------------------------(5分)
在Rt△ABE中,由tan∠EAB=
=
,AB=2得BE=
------------(6分)
在Rt△ABC中∵BC=
=
(0<x<2)
∴S△ABC=
AC•BC=
x
------------------------------------(7分)
∴V(x)=VC-ABE=VE-ABC=
S△ABC•BE=
x
(0<x<2)-------(8分)
(3)由(2)知要V(x)取得最大值,当且仅当x
=
取得最大值,
∵0<x<2
∴x2(4-x2)≤(
)2=4------------(10分)
∴当且仅当x2=4-x2,即..时,“=”成立,
即当V(x)取得最大值时AC=
,这时△ACB为等腰直角三角形
连接DB,∵AC=BC,DC=DC
∴Rt△DCA≌Rt△DCB------------------(12分)
∴AD=BD 又四边形BCDE为矩形
∴BD=CE
∴AD=CE------------------------------------------------------------(14分)

(1)证明:∵四边形DCBE为平行四边形∴CD∥BE,BC∥DE---------(1分)
∵DC⊥平面ABC,BC?平面ABC∴DC⊥BC.----------(2分)
∵AB是圆O的直径∴BC⊥AC且DC∩AC=C
∴BC⊥平面ADC.
∵DE∥BC∴DE⊥平面ADC---------------------------------------(3分)
又∵DE?平面ADE∴平面ACD⊥平面ADE----------------(4分)
(2)∵DC⊥平面ABC,CD∥BE∴BE⊥平面ABC
∵AB?平面ABC∴BE⊥AB,--------------------------------------------------------(5分)
在Rt△ABE中,由tan∠EAB=
| BE |
| AB |
| ||
| 2 |
| 3 |
在Rt△ABC中∵BC=
| AB2-AC2 |
| 4-x2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 4-x2 |
∴V(x)=VC-ABE=VE-ABC=
| 1 |
| 3 |
| ||
| 6 |
| 4-x2 |
(3)由(2)知要V(x)取得最大值,当且仅当x
| 4-x2 |
| x2(4-x2) |
∵0<x<2
∴x2(4-x2)≤(
| x2+4-x2 |
| 2 |
∴当且仅当x2=4-x2,即..时,“=”成立,
即当V(x)取得最大值时AC=
| 2 |
连接DB,∵AC=BC,DC=DC
∴Rt△DCA≌Rt△DCB------------------(12分)
∴AD=BD 又四边形BCDE为矩形
∴BD=CE
∴AD=CE------------------------------------------------------------(14分)
点评:本题考查面面垂直的判定,锥体体积公式,基本不等式法求函数最值,考查空间想象能力、转化(垂直、平行及两者之间的转化)、论证、计算能力.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
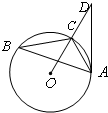 如图,已知△ABC内接于⊙O,点D在OC的延长线上,AD切⊙O于A,若∠ABC=30°,AC=2,则AD的长为
如图,已知△ABC内接于⊙O,点D在OC的延长线上,AD切⊙O于A,若∠ABC=30°,AC=2,则AD的长为 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2, 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DBCE为平行四边形,EC⊥平面ABC,AB=2AC=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DBCE为平行四边形,EC⊥平面ABC,AB=2AC=2, 如图,已知△ABC内接于圆⊙O,点D在OC的延长线上,AD是⊙O的切线,若∠B=30°,AC=
如图,已知△ABC内接于圆⊙O,点D在OC的延长线上,AD是⊙O的切线,若∠B=30°,AC=