题目内容
已知命题p:x1、x2是方程x2-mx-2=0的两个实根,不等式a2-5a-3≥ 对任意实数m∈[-1,1]恒成立;命题q:不等式ax2+2x-1>0有解。若命题p是真命题,命题q为假命题,求实数a的取值范围。
对任意实数m∈[-1,1]恒成立;命题q:不等式ax2+2x-1>0有解。若命题p是真命题,命题q为假命题,求实数a的取值范围。
 对任意实数m∈[-1,1]恒成立;命题q:不等式ax2+2x-1>0有解。若命题p是真命题,命题q为假命题,求实数a的取值范围。
对任意实数m∈[-1,1]恒成立;命题q:不等式ax2+2x-1>0有解。若命题p是真命题,命题q为假命题,求实数a的取值范围。a≤-1
试题分析:解:∵
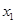 ,
,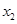 是方程x2-mx-2=0的两个实根,∴
是方程x2-mx-2=0的两个实根,∴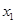 +
+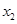 =m,
=m,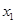
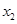 =-2,∴|
=-2,∴|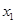 -
-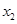 |=
|=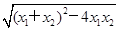
=
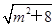 ,又m∈[-1,1],∴|
,又m∈[-1,1],∴|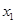 -
-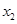 |的最大值等于3。 3分
|的最大值等于3。 3分由题意得到:a2-5a-3≥3
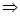 a≥6,a≤-1;命题p是真命题时,a≥6,a≤-1 5分。
a≥6,a≤-1;命题p是真命题时,a≥6,a≤-1 5分。命题q:(1)a>1时,ax2+2x-1>0显然有解;(2)a=0时,2x-1>0有解;(3)a<0时,△=4+4a>0,
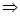 -1<a<0 9分;从而命题q为真命题时:a>-1 10分
-1<a<0 9分;从而命题q为真命题时:a>-1 10分∴命题p是真命题,命题q为假命题时实数a的取值范围是 a≤-1 12分
点评:主要是考查了复合命题的真值以及不等式的解集的运用,属于中档题。

练习册系列答案
相关题目
 ,且
,且 ,则( )
,则( )



 对一切实数
对一切实数 恒成立,则实数
恒成立,则实数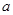 的取值范围是 .
的取值范围是 . 的解为
的解为 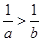 ,则a<b
,则a<b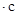
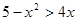 的解集为( )
的解集为( ) 满足
满足 ,则
,则 的大小关系是( )
的大小关系是( )



 的不等式
的不等式 ,此不等式的解集为
,此不等式的解集为 ,求实数
,求实数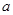 的取值范围。
的取值范围。 满足
满足 ,
, ,
, ,求表达式
,求表达式 的值.
的值.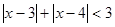 ;
;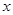 的不等式
的不等式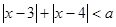 的解集不是空集,求实数
的解集不是空集,求实数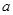 的取值范围.
的取值范围.