题目内容
对于定义域为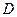 的函数
的函数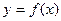 ,若同时满足下列条件:
,若同时满足下列条件:
①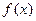 在
在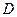 内单调递增或单调递减;②存在区间
内单调递增或单调递减;②存在区间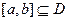 ,使
,使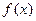 在
在 上的值域为
上的值域为 ;那么把
;那么把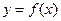
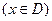 叫闭函数.
叫闭函数.
(1)求闭函数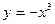 符合条件②的区间
符合条件②的区间 ;
;
(2)判断函数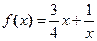 ,
,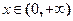 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)若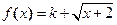 是闭函数,求实数
是闭函数,求实数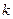 的范围?
的范围?
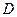 的函数
的函数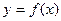 ,若同时满足下列条件:
,若同时满足下列条件:①
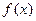 在
在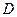 内单调递增或单调递减;②存在区间
内单调递增或单调递减;②存在区间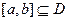 ,使
,使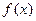 在
在 上的值域为
上的值域为 ;那么把
;那么把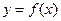
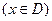 叫闭函数.
叫闭函数.(1)求闭函数
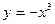 符合条件②的区间
符合条件②的区间 ;
;(2)判断函数
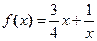 ,
,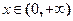 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;(3)若
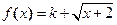 是闭函数,求实数
是闭函数,求实数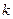 的范围?
的范围?(1)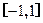
(2)不是闭函数.
(3)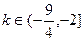
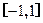
(2)不是闭函数.
(3)
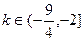
(1)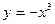 在
在 上递减,依题意,
上递减,依题意,
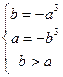 解得
解得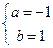
∴所求的区间为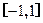 .
.
(2)当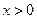 时,
时,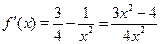 .
.
当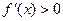 时,得
时,得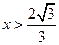 ;
;
当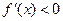 时,得
时,得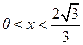 ,
,
∴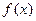 的递增区间为
的递增区间为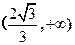 ,递减区间为
,递减区间为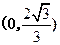
∴函数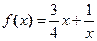 在定义域
在定义域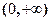 上不单调递增或单调递减,
上不单调递增或单调递减,
故函数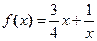 ,
,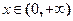 不是闭函数.
不是闭函数.
(3)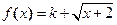 在定义域
在定义域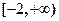 上为增.
上为增.
若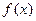 是闭函数,则存在区间
是闭函数,则存在区间 ,在区间
,在区间 上,函数
上,函数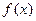 的值域为
的值域为 ,即
,即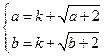
∴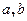 为方程
为方程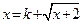 (*)的两个实数根,
(*)的两个实数根,
即方程 有两个不等的实根
有两个不等的实根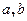 ,
,
令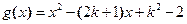
当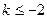 时,有
时,有 即
即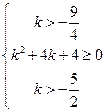
解得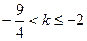 .
.
当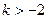 时,有
时,有 即
即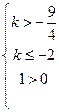
此不等式组无解.
综上所述,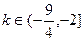 .
.
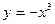 在
在 上递减,依题意,
上递减,依题意,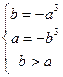 解得
解得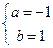
∴所求的区间为
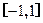 .
.(2)当
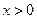 时,
时,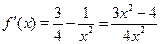 .
.当
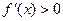 时,得
时,得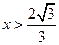 ;
;当
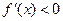 时,得
时,得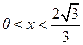 ,
,∴
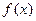 的递增区间为
的递增区间为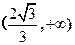 ,递减区间为
,递减区间为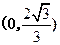
∴函数
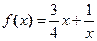 在定义域
在定义域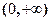 上不单调递增或单调递减,
上不单调递增或单调递减,故函数
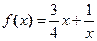 ,
,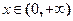 不是闭函数.
不是闭函数.(3)
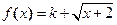 在定义域
在定义域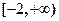 上为增.
上为增.若
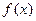 是闭函数,则存在区间
是闭函数,则存在区间 ,在区间
,在区间 上,函数
上,函数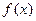 的值域为
的值域为 ,即
,即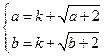
∴
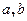 为方程
为方程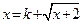 (*)的两个实数根,
(*)的两个实数根,即方程
 有两个不等的实根
有两个不等的实根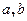 ,
,令
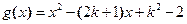
当
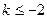 时,有
时,有 即
即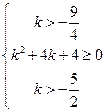
解得
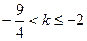 .
.当
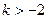 时,有
时,有 即
即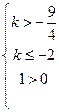
此不等式组无解.
综上所述,
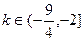 .
.
练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
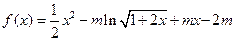 ,其中
,其中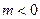 .
.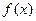 的单调性;
的单调性;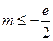 (其中
(其中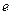 是自然对数的底数)时,在
是自然对数的底数)时,在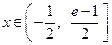 上至少
上至少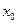 ,使
,使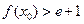 成立,求
成立,求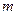 的取值范围;
的取值范围;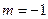 时,对任意
时,对任意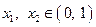 ,
,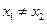 ,有
,有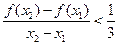 .
.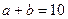 ,cosC是方程
,cosC是方程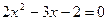 的一个根,求△ABC周长的最小值。
的一个根,求△ABC周长的最小值。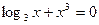 在区间
在区间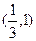 内的实数根的个数是.
内的实数根的个数是.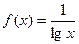 在
在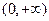 是减函数;
是减函数;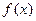 的定义域为
的定义域为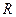 ,
,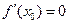 是
是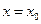 为极值点的既不充分又不必要条件;
为极值点的既不充分又不必要条件;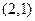 的距离与到定直线
的距离与到定直线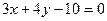 的距离相等的点的轨迹是抛物线;
的距离相等的点的轨迹是抛物线;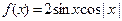 的最小正周期是
的最小正周期是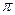 ;
;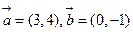 ,则
,则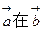 方向上的投影为4.
方向上的投影为4.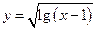 的定义域是( )
的定义域是( )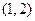
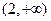
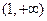
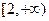
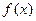 满足
满足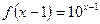 ,则函数
,则函数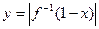 的图象是( )
的图象是( )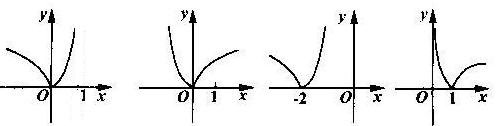
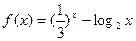 ,
,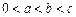 ,
,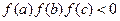 ,实数
,实数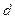 是函数
是函数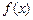 的一个零点.给出下列四个判断:
的一个零点.给出下列四个判断: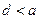 ;②
;②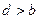 ;③
;③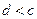 ;④
;④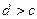 .
.