Question

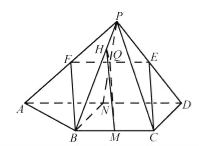
【题目】（本题满分15分）如图，已知四棱锥P–ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点.

（Ⅰ）证明：CE∥平面PAB；

（Ⅱ）求直线CE与平面PBC所成角的正弦值.

Answer 1

【答案】（Ⅰ）见解析；（Ⅱ）.

【解析】本题主要考查空间点、线、面位置关系，直线与平面学科&网所成的角等基础知识，同时考查空间想象能力和运算求解能力。满分15分。

（Ⅰ）如图，设PA中点为F，连结EF，FB.

因为E，F分别为PD，PA中点，所以EF∥AD且，

又因为BC∥AD，，所以

EF∥BC且EF=BC，

即四边形BCEF为平行四边形，所以CE∥BF，

因此CE∥平面PAB.

（Ⅱ）分别取BC，AD的中点为M，N.连结PN交EF于点Q，连结MQ.

因为E，F，N分别是PD，PA，AD的中点，所以Q为EF中点，

在平行四边形BCEF中，MQ∥CE.

由△PAD为等腰直角三角形得

PN⊥AD.

由DC⊥AD，N是AD的中点得

BN⊥AD.

所以 AD⊥平面PBN，

由BC∥AD得 BC⊥平面PBN，

那么，平面PBC⊥平面PBN.

过点Q作PB的垂线，垂足为H，连结MH.

MH是MQ在平面PBC上的射影，所以∠QMH是直线CE与平面PBC所成的角.

设CD=1.

在△PCD中，由PC=2，CD=1，PD=得CE=，

在△PBN中，由PN=BN=1，PB=得QH=，

在Rt△MQH中，QH=，MQ=，

所以sin∠QMH=，

所以，直线CE与平面PBC所成角的正弦值是.