Question

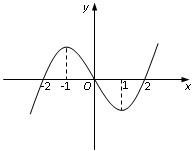在R上可导的函数f（x）的图象如图所示，则关于x的不等式x•f′（x）＜0的解集为

1. A.
   （-1，0）∪（1，+∞）
2. B.
   （-∞，-1）∪（0，1）
3. C.
   （-2，-1）∪（1，2）
4. D.
   （-∞，-2）∪（2，+∞）

Answer 1

B
分析：通过图象得到函数的单调性，从而得到导数在某区间的符合，通过讨论x的符号求解不等式即可．
解答：由图象可知f′（x）=0的解为x=-1和x=1
函数f（x）在（-∞，-1）上增，在（-1，1）上减，在（1，+∞）上增
∴f′（x）在（-∞，-1）上大于0，在（-1，1）小于0，在（1，+∞）大于0
当x＜0时，f′（x）＞0解得x∈（-∞，-1）
当x＞0时，f′（x）＜0解得x∈（0，1）
综上所述，x∈（-∞，-1）∪（0，1），
故选B．
点评：本题考查了函数的图象，导数的运算以及其他不等式的解法，分类讨论的思想的渗透，本题属于基础题．