题目内容
以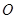 为中心,
为中心,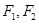 为两个焦点的椭圆上存在一点
为两个焦点的椭圆上存在一点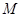 ,满足
,满足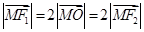 ,则该椭圆的离心率为
,则该椭圆的离心率为
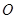 为中心,
为中心,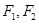 为两个焦点的椭圆上存在一点
为两个焦点的椭圆上存在一点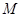 ,满足
,满足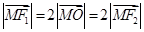 ,则该椭圆的离心率为
,则该椭圆的离心率为A. | B.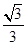 | C.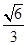 | D. |
C
试题分析:根据题意,由于以
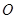 为中心,
为中心,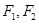 为两个焦点的椭圆上存在一点
为两个焦点的椭圆上存在一点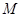 ,满足
,满足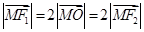 ,且根据定义可设|MO|=1,且根据中线长度的公式得到a, b,c的关系式,
,且根据定义可设|MO|=1,且根据中线长度的公式得到a, b,c的关系式,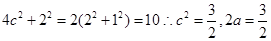 进而得到离心率为
进而得到离心率为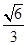 ,故选C.
,故选C.点评:解决的关键是根据椭圆的定义以及焦点三角形的性质来求解离心率,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
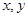 )及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为
)及两个定点A(-2,0),B(2,0),直线PA、PB的斜率分别为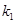 、
、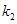 且
且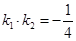
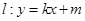 与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线
与曲线C交于不同的两点M、N,当OM⊥ON时,求点O到直线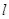 的距离。(O为坐标原点)
的距离。(O为坐标原点)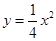 的焦点坐标是( )
的焦点坐标是( )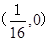
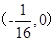
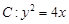 ,的焦点为F,直线
,的焦点为F,直线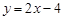 与抛物线C交于A、B两点,则
与抛物线C交于A、B两点,则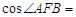 ( )
( )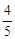
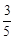


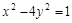 的渐近线为
的渐近线为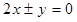
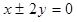
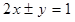
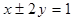
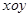 和极坐标系
和极坐标系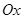 的原点与极点重合,
的原点与极点重合,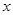 轴的正半轴与极轴重合,单位长度相同。已知曲线
轴的正半轴与极轴重合,单位长度相同。已知曲线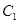 的极坐标方程为
的极坐标方程为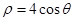 ,曲线
,曲线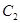 的参数方程为
的参数方程为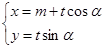
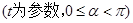 ,射线
,射线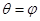 ,
,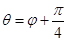 ,
,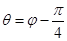 与曲线
与曲线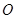 以外的三点A,B,C.
以外的三点A,B,C.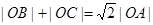 ;
;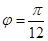 时,B,C两点在曲线
时,B,C两点在曲线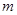 与
与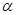 的值。
的值。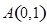 、
、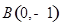 ,
, 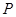 是一个动点, 且直线
是一个动点, 且直线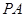 、
、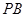 的斜率之积为
的斜率之积为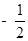 .
.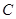 的方程;
的方程; 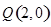 , 过点
, 过点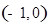 的直线
的直线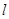 交
交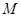 、
、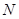 两点, 若对满足条件的任意直线
两点, 若对满足条件的任意直线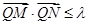 恒成立, 求
恒成立, 求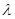 的最小值.
的最小值.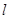 :
: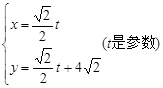 上的点向圆C:
上的点向圆C: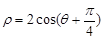 引切线,
引切线,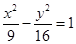 的一个焦点到一条渐近线的距离为______________
的一个焦点到一条渐近线的距离为______________