题目内容
函数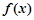 定义在区间
定义在区间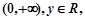 都有
都有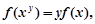 且
且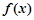 不恒为零.
不恒为零.
(1)求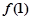 的值;
的值;
(2)若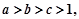 且
且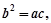 求证:
求证: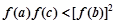 ;
;
(3)若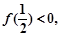 求证:
求证: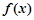 在
在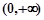 上是增函数.
上是增函数.
(1)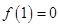 .(2)(3)见解析
.(2)(3)见解析
解析试题分析:(1)通过带特殊值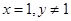 可求得;(2)设
可求得;(2)设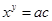 ,同取以
,同取以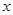 为底的对数得
为底的对数得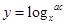 ,
,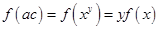 ,把
,把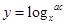 代入在运用对数运算性质就可得
代入在运用对数运算性质就可得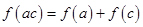 ,有
,有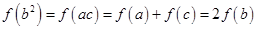 ,所以
,所以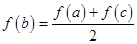 ,要证
,要证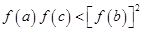 只需证
只需证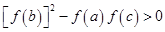 ,由以上很容易得到
,由以上很容易得到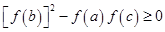 ,需要证出
,需要证出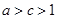 时,
时,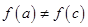 即等号不成立;(3)设
即等号不成立;(3)设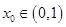 ,则
,则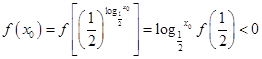 ,所以得
,所以得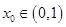 时,
时,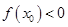 ,任取
,任取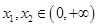 ,
,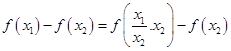 得证.
得证.
试题解析:⑴令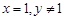 ,
,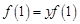 ,
,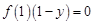 ,
,
因为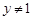 ,所以
,所以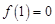 . 3分
. 3分
⑵设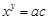 ,则
,则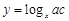 ,所以
,所以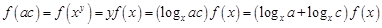
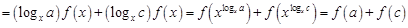 , 5分
, 5分
因为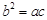 ,所以
,所以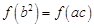 ,所以
,所以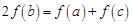 ,
,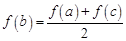 ,
,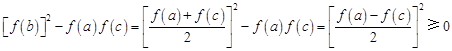 . 8分
. 8分
下面证明当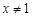 时,
时,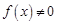 .
.
假设存在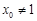 ,
,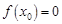 ,则对于任意
,则对于任意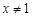 ,
,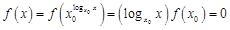 ,不合题意.所以,当
,不合题意.所以,当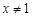 时,
时,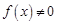 .
.
因为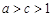 ,所以存在
,所以存在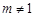 ,
, ,
,
所以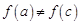 ,所以
,所以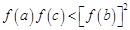 . 10分
. 10分
⑶设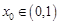 ,则
,则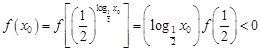 , 12分
, 12分
设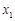 ,
, 为区间
为区间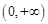 内的任意两个值,且
内的任意两个值,且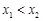 ,则
,则 ,由⑵的证明知,
,由⑵的证明知,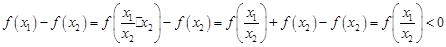 ,
,
所以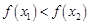 ,所以
,所以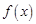 在
在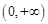 上是增函数. 16分
上是增函数. 16分
考点:1.函数附特殊值法;2.函数的构造法;3.证明单调函数.

练习册系列答案
相关题目
辽宁号航母纪念章从2012年10月5日起开始上市.通过市场调查,得到该纪念章每1枚的市场价 (单位:元)与上市时间
(单位:元)与上市时间 (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 天 天 | 4 | 10 | 36 |
市场价 元 元 | 90 | 51 | 90 |
 与上市时间
与上市时间 的变化关系并说明理由:①
的变化关系并说明理由:①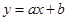 ;②
;②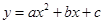 ;③
;③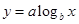 .
.(2)利用你选取的函数,求辽宁号航母纪念章市场价最低时的上市天数及最低的价格.
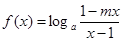 是奇函数,(其中
是奇函数,(其中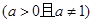 )
)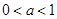 时,讨论函数f(x)的增减性;
时,讨论函数f(x)的增减性; 时,f(x)的值域是(1,
时,f(x)的值域是(1,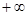 ),求n与a的值。
),求n与a的值。 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点 米,圆心角为
米,圆心角为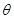 (弧度).
(弧度).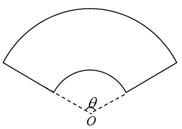
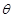 关于
关于 ,求
,求 的函数关系式,并求出
的函数关系式,并求出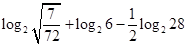 ;
;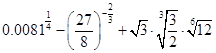 .
.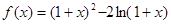
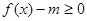 在
在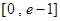 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;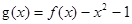 ,若关于x的方程
,若关于x的方程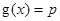 至少有一个解,求p的最小值.
至少有一个解,求p的最小值.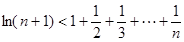
 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点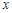 米,圆心角为
米,圆心角为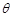 (弧度).
(弧度).
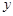 ,求
,求