题目内容
2.已知函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x}(x>0)}\\{{x}^{3}+3(x≤0)}\end{array}\right.$,则函数y=f(2x2+x)-a(a>2)的零点个数可能是4,5,6.分析 作函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x}(x>0)}\\{{x}^{3}+3(x≤0)}\end{array}\right.$与函数y=2x2+x的图象,从而讨论以确定函数的零点的个数.
解答 解:作函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x}(x>0)}\\{{x}^{3}+3(x≤0)}\end{array}\right.$与函数y=2x2+x的图象如下,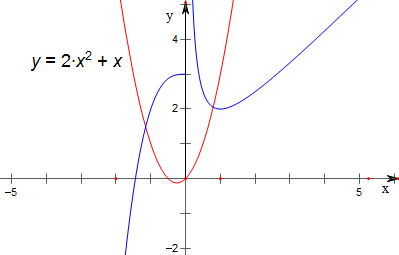
二次函数y=2x2+x的值域为[-$\frac{1}{8}$,+∞),
故2x2+x+$\frac{1}{2{x}^{2}+x}$-a=0有四个解;
由(2x2+x)3+3-a=0得,
a=(2x2+x)3+3,
故当2<a<3-$\frac{1}{{8}^{3}}$时,(2x2+x)3+3-a=0无解,
当a=3-$\frac{1}{{8}^{3}}$时,(2x2+x)3+3-a=0有且只有一个解,
当3-$\frac{1}{{8}^{3}}$<a≤3时,(2x2+x)3+3-a=0有且只有两个解;
综上所述,函数y=f(2x2+x)-a(a>2)的零点个数可能是4,5,6;
故答案为:4,5,6.
点评 本题考查了分段函数的应用及复合函数的应用,同时考查了函数的零点与方程的根的关系应用,属于中档题.

练习册系列答案
相关题目
13.已知圆M:4x2+4y2+8x+16y-5=0直线l:x+y-1=0,△ABC的顶点A在直线l上,顶点B,C都在圆M上,且边AB过圆心M,∠BAC=45°,则点A横坐标的最大值为( )
| A. | $\frac{5}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
5.某研究小组为了研究中学生的身体发育情况,在某学校随机抽出20名15至16周岁的男生,将他们的身高和体重制成2×2的列联表,根据列联表的数据,判断该学校15至16周岁的男生的身高和体重之间在犯错误概率不超过0.025的前提下有关系.
附:独立性检验临界值表
k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 超重 | 不超重 | 总计 | |
| 偏高 | 1 | 1 | 5 |
| 不偏高 | 3 | 12 | 15 |
| 总计 | 7 | 12 | 20 |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
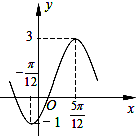 已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<π)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<π)的部分图象如图所示.