题目内容
20.已知函数f(x)=$\frac{{\sqrt{3}}}{2}$sin2x-cos2x-$\frac{1}{2}$,x∈R.(Ⅰ)当x∈[-$\frac{π}{12}$,$\frac{5π}{12}}$]时,求函数f(x)的最小值和最大值;
(Ⅱ)将函数y=f(x)的图象的横坐标伸长为原来的2倍,再将函数图象向上平移1个单位,得到函数y=g(x),求函数y=|g(x)|的单调增区间.
分析 (Ⅰ)利用二倍角公式以及两角和的正弦函数化简函数的解析式,求出相位的范围,利用三角函数的有界性求解即可.
(Ⅱ)利用三角函数的图象变换求出函数的解析式,利用函数的单调性求解函数的单调性即可.
解答 解:(Ⅰ)$f(x)=\frac{{\sqrt{3}}}{2}sin2x-{cos^2}x-\frac{1}{2}=\frac{{\sqrt{3}}}{2}sin2x-\frac{1-cos2x}{2}-\frac{1}{2}$=$sin(2x-\frac{π}{6})-1$--------(4分)
由$x∈[-\frac{π}{12},\frac{5π}{12}]$,∴$2x-\frac{π}{6}∈$$[-\frac{π}{3},\frac{2π}{3}]$,
∴$x=-\frac{π}{12},f(x)$的最小值为$-1-\frac{{\sqrt{3}}}{2},x=\frac{π}{3}$,
f(x)的最大值是0.--------(4分)
(Ⅱ)解:将函数y=f(x)=$sin(2x-\frac{π}{6})-1$的图象的横坐标伸长为原来的2倍,得到函数y=$sin(x-\frac{π}{6})-1$,再将函数图象向上平移1个单位,得到函数y=g(x)=$sin(x-\frac{π}{6})$,
即$g(x)=sin(x-\frac{π}{6})$---------(3分)
y=|$sin(x-\frac{π}{6})$|,由$kπ≤x-\frac{π}{6}≤\frac{π}{2}+kπ,k∈Z$-------(2分)
得:增区间为$[\frac{π}{6}+kπ,\frac{2π}{3}+kπ],k∈Z$-------(2分)
点评 本题考查三角函数的最值以及三角函数的解析式的求法,三角函数的图象的变换,考查分析问题解决问题到哪里.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既非充分又非必要 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
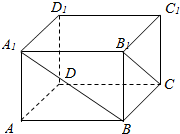 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3.
在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3.