Question

9．椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）上存在一点 P满足$∠{A}{P}F=\frac{π}{2}$，F为椭圆的左焦点，A为椭圆的右顶点，则椭圆的离心率的范围是（　　）

• A． $（{0，\frac{1}{2}}）$
• B． $（{0，\frac{{\sqrt{2}}}{2}}）$
• C． $（{\frac{1}{2}，1}）$
• D． $（{\frac{{\sqrt{2}}}{2}，1}）$

Answer 1

分析 由题意求出以FA为直径的圆的方程，联立圆与椭圆方程，求出点P的坐标，由P得横坐标满足-c＜x_P＜a求解．

解答 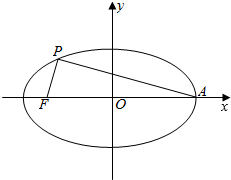解：如图，
A（a，0），F（-c，0），
以FA为直径的圆的方程为$（x-\frac{a-c}{2}）^{2}+{y}^{2}=（\frac{a+c}{2}）^{2}$，
整理得：x²-（a-c）x+y²-ac=0．
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\\{{x}^{2}-（a-c）x+{y}^{2}-ac=0}\end{array}\right.$，消去y得：c²x²-a²（a-c）x+a²（b²-ac）=0．
由题意可得：a，x_P为方程c²x²-a²（a-c）x+a²（b²-ac）=0的两根．
由根与系数的关系可得：${x}_{P}+a=\frac{{a}^{2}（a-c）}{{c}^{2}}$，
∴${x}_{P}=\frac{{a}^{2}（a-c）}{{c}^{2}}-a=\frac{{a}^{3}-{a}^{2}c-a{c}^{2}}{{c}^{2}}$．
由图可知：-c＜x_P＜a．
即$-c＜\frac{{a}^{3}-{a}^{2}c-a{c}^{2}}{{c}^{2}}＜a$，
化简左边可得（a-c）²＞0恒成立；
化简右边可得2e²+e-1＞0，解得e＜-1或e$＞\frac{1}{2}$．
又0＜e＜1，∴$\frac{1}{2}＜e＜1$．
故选：C．

点评 本题考查了椭圆的标准方程与简单几何性质，圆与圆锥曲线位置关系的应用问题，解题的关键是得到关于a，c的等式，体现了数学转化思想方法，属中档题．