题目内容
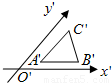
直角三角形ABC的斜边AB在平面α内,AC,BC与平面α分别成30°,45°的角,若S△ABC=10,则△ABC在平面α内的射影构成的三角形的面积为分析:过点C作CH⊥平面α,设CH=h,用h表示三角形ABC的边AB、AC、BC、ABC的斜边AB上的高为x,求出角三角形ABC与平面α成的角为β的正弦值,从而求出β的余弦值,β的余弦值等于射影面积比上直角三角形ABC的面积.
解答:解:过点C作CH⊥平面α,设CH=h,∵AC,BC与平面α分别成30°,45°的角,
∴BC=
h,AC=2h,AB=
h,∵直角三角形ABC的斜边AB在平面α内,
S△=
BC•AC=10,∴h=
,设直角三角形ABC的斜边AB上的高为x,
由面积法可求 x=
,设直角三角形ABC与平面α成的角为β,
sinβ=
=
,∴β=600,cos600=
=
=
,
∴S′=5,即△ABC在平面α内的射影构成的三角形的面积为5;
故答案为5.
∴BC=
| 2 |
| 6 |
S△=
| 1 |
| 2 |
5
|
由面积法可求 x=
| 2 |
| 3 |
15
|
sinβ=
| h |
| x |
| ||
| 2 |
| 1 |
| 2 |
| S′′ |
| S△ABC |
| S′ |
| 10 |
∴S′=5,即△ABC在平面α内的射影构成的三角形的面积为5;
故答案为5.
点评:本题考查直线与平面所成的角,三角形ABC与平面α成的角余弦值等于射影面积比上直角三角形ABC的面积.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 ABC的三个顶点是A(-a,0)、B(a,0)和C(
ABC的三个顶点是A(-a,0)、B(a,0)和C( ,
, a),则
a),则
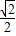 ,则其原面积为 .
,则其原面积为 .