Question

【题目】如图，设H为锐角△ABC的垂心.由顶点A向以BC为直径的⊙O作一条切线AE，切点为E，联结EH交AO于点G，过G任意作⊙O的一条弦PQ.证明：AO 平分∠PAQ.

Answer 1

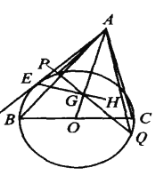
【答案】见解析

【解析】

如图，

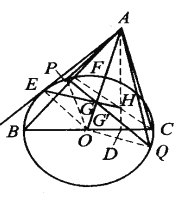
设AD、CF是△ABC的两条高，于是，F在⊙O上，因为∠BFC=∠ADB=90°，

所以，B、F、H、D四点共圆.

由割线定理得.

联结OE，则OE⊥AE.于是，有.

所以，.①

过点E作.垂足为，联结.

在Rt△AEO中，由射影定理得.②

由式①、②得.

则O、D、H、四点共圆.

故.从而，.

因此，E、、H三点共线，即点G与重合.

所以，EH⊥AO.

联结OP、OQ.在⊙O中，由EH⊥AO及相交弦定理得：

.

则A、P、O、Q四点共圆.

又OP=OQ，所以，∠PAO=∠QAO.