题目内容
 设P(t,t2)是抛物线y=x2(0<x<1)上的一个动点,过P作抛物线的切线与x轴及直线x=1相交于A、B如图所示,若△PAC,△PBC的面积分别为g(t)和h(t).
设P(t,t2)是抛物线y=x2(0<x<1)上的一个动点,过P作抛物线的切线与x轴及直线x=1相交于A、B如图所示,若△PAC,△PBC的面积分别为g(t)和h(t).(1)求g(t)、h(t);
(2)记号max(a1,a2,…an)表示数a1,a2,…an中最大的那个数.设f(t)=max(g(t),h(t))试求f(t)的极大值与极小值.
考点:利用导数研究曲线上某点切线方程,函数的最值及其几何意义,数列与函数的综合
专题:计算题,导数的综合应用,直线与圆
分析:(1)求出函数的导数,求得切线的斜率,切线方程,再求A,B的坐标,以及三角形PAC,PBC的面积,即可得到g(t),h(t);
(2)对g(t),h(t)作差,讨论,即可得到f(t),再求导数,求单调区间,进而得到极值.
(2)对g(t),h(t)作差,讨论,即可得到f(t),再求导数,求单调区间,进而得到极值.
解答:
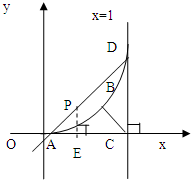 解:(1)由于y=x2(0<x<1)的导数y′=2x,
解:(1)由于y=x2(0<x<1)的导数y′=2x,
过点P(t,t2)的抛物线的切线PA的斜率为2t,
于是其方程为y-t2=2t(x-t)
令x=1,得y=2t-t2令y=0则x=
,
则A(
,0),B(1,2t-t2),
所以△PAC与△PBC的面积为:
S△PAC=
AC•EP=
(1-
)•t2,
S△PBC=
CB•EC=
(2t-t2)(1-t),0<t<1,
则g(t)=-
t3+
t2,h(t)=
t3-
t2+t,0<t<1,
(2)由g(t)-h(t)=
t2(2-t)-
t(1-t)(2-t)
=
t(2-t)[t-2(1-t)]=
t(2-t)(3t-2),0<t<1
故当0<t<
时,g(t)<h(t)因此f(t)=h(t),
当
≤t≤1时,h(t)≤g(t),因此f(t)=g(t),
即f(t)=
,
于是,当0<t<
时,由f′(t)=
(3t2-6t+2)=0,
解得t=1-
,可知此乃f(t)的极大值点,
所以极大值是f(1-
)=
,无极小值.
当
≤t<1时,由f′(t)=
(4t-3t2)=t(1-
t)>0恒成立,
可知f(t)是单调增加的,因此它的极小值是f(
)=
,无极大值.
综上,当t=1-
时f(t)取极大值
,当t=
时f(t)取极小值
.
 解:(1)由于y=x2(0<x<1)的导数y′=2x,
解:(1)由于y=x2(0<x<1)的导数y′=2x,过点P(t,t2)的抛物线的切线PA的斜率为2t,
于是其方程为y-t2=2t(x-t)
令x=1,得y=2t-t2令y=0则x=
| t |
| 2 |
则A(
| t |
| 2 |
所以△PAC与△PBC的面积为:
S△PAC=
| 1 |
| 2 |
| 1 |
| 2 |
| t |
| 2 |
S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
则g(t)=-
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(2)由g(t)-h(t)=
| 1 |
| 4 |
| 1 |
| 2 |
=
| 1 |
| 4 |
| 1 |
| 4 |
故当0<t<
| 2 |
| 3 |
当
| 2 |
| 3 |
即f(t)=
|
于是,当0<t<
| 2 |
| 3 |
| 1 |
| 2 |
解得t=1-
| ||
| 3 |
所以极大值是f(1-
| ||
| 3 |
| ||
| 9 |
当
| 2 |
| 3 |
| 1 |
| 4 |
| 3 |
| 4 |
可知f(t)是单调增加的,因此它的极小值是f(
| 2 |
| 3 |
| 4 |
| 27 |
综上,当t=1-
| ||
| 3 |
| ||
| 9 |
| 2 |
| 3 |
| 4 |
| 27 |
点评:本题考查导数的运用:求切线方程,求单调区间和求极值,考查三角形的面积公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
y=tanx的最小正周期为( )
A、
| ||
| B、π | ||
| C、2π | ||
| D、-π |
极坐标方程ρ=10sinθ表示( )
A、以(10,
| ||
| B、以(5,0)为圆心,5为半径的圆 | ||
| C、以(10,0)为圆心,5为半径的圆 | ||
D、以(5,
|
函数f(x))满足(x+2)=
,若f(1)=2,则f(99)=( )
| 1 |
| f(x) |
| A、1 | ||
| B、3 | ||
C、
| ||
D、
|
函数f(x)=(
sinx-cosx)cosx的值域是( )
| 3 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|