题目内容
若正三棱柱 的棱长均相等,则
的棱长均相等,则 与侧面
与侧面 所成角的正切值为___.
所成角的正切值为___.
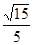
解析试题分析:设棱长为1.取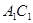 中点
中点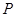 ,连接
,连接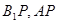 ,根据正三棱柱的特点,
,根据正三棱柱的特点,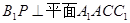 ,根据线面角的定义可知,
,根据线面角的定义可知,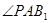 为
为 与侧面
与侧面 所成角,在
所成角,在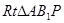 中,
中,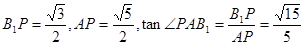 .
.
考点:线面角的定义.

练习册系列答案
相关题目
题目内容
若正三棱柱 的棱长均相等,则
的棱长均相等,则 与侧面
与侧面 所成角的正切值为___.
所成角的正切值为___.
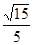
解析试题分析:设棱长为1.取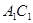 中点
中点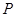 ,连接
,连接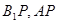 ,根据正三棱柱的特点,
,根据正三棱柱的特点,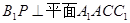 ,根据线面角的定义可知,
,根据线面角的定义可知,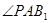 为
为 与侧面
与侧面 所成角,在
所成角,在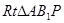 中,
中,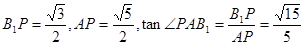 .
.
考点:线面角的定义.
